题目内容
在直角坐标系中,O为坐标原点,直线l经过点P(3,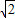 )及双曲线
)及双曲线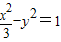 的右焦点F.
的右焦点F.(1)求直线l的方程;
(2)如果一个椭圆经过点P,且以点F为它的一个焦点,求椭圆的标准方程;
(3)若在(1)、(2)情形下,设直线l与椭圆的另一个交点为Q,且
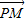 =λ
=λ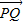 ,当|
,当|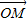 |最小时,求λ的值.
|最小时,求λ的值.
【答案】分析:(1)确定双曲线的右焦点坐标,利用两点式,可求方程;
(2)设出椭圆的标准方程,利用焦点坐标及点P在椭圆上,求出几何量,即可得到椭圆的标准方程;
(3)直线方程,代入椭圆方程,求出Q的坐标,进而可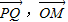 的坐标,求模长,利用配方法求最值,即可得到结论.
的坐标,求模长,利用配方法求最值,即可得到结论.
解答:解:(1)由题意双曲线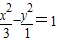 的右焦点为F(2,0)
的右焦点为F(2,0)
∵直线l经过点P(3,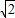 ),F(2,0)
),F(2,0)
∴根据两点式,得所求直线l的方程为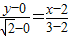
即y=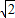 (x-2).
(x-2).
∴直线l的方程是y=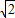 (x-2).
(x-2).
(2)设所求椭圆的标准方程为
∵一个焦点为F(2,0)
∴c=2,即a2-b2=4 ①
∵点P(3,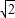 )在椭圆上,
)在椭圆上,
∴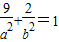 ②
②
由①②解得a2=12,b2=8
所以所求椭圆的标准方程为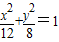 ;
;
(3)由题意,直线方程代入椭圆方程可得x2-3x=0
∴x=3或x=0
∴y= 或y=-2
或y=-2
∴Q(0,-2 )
)
∴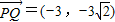
∴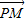 =λ
=λ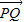 =
=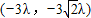 ,
,
∴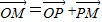 =
=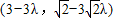
∴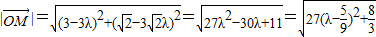
∴当λ= 时,
时,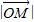 最小.
最小.
点评:本题考查直线与椭圆的方程,考查向量知识,考查学生分析解决问题的能力,属于中档题.
(2)设出椭圆的标准方程,利用焦点坐标及点P在椭圆上,求出几何量,即可得到椭圆的标准方程;
(3)直线方程,代入椭圆方程,求出Q的坐标,进而可
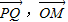 的坐标,求模长,利用配方法求最值,即可得到结论.
的坐标,求模长,利用配方法求最值,即可得到结论.解答:解:(1)由题意双曲线
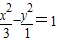 的右焦点为F(2,0)
的右焦点为F(2,0)∵直线l经过点P(3,
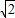 ),F(2,0)
),F(2,0)∴根据两点式,得所求直线l的方程为
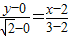
即y=
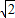 (x-2).
(x-2).∴直线l的方程是y=
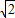 (x-2).
(x-2).(2)设所求椭圆的标准方程为

∵一个焦点为F(2,0)
∴c=2,即a2-b2=4 ①
∵点P(3,
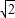 )在椭圆上,
)在椭圆上,∴
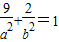 ②
②由①②解得a2=12,b2=8
所以所求椭圆的标准方程为
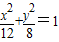 ;
;(3)由题意,直线方程代入椭圆方程可得x2-3x=0
∴x=3或x=0
∴y=
 或y=-2
或y=-2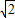
∴Q(0,-2
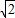 )
) ∴
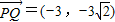
∴
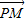 =λ
=λ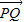 =
=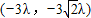 ,
,∴
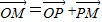 =
=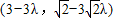
∴
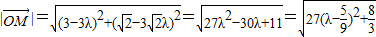
∴当λ=
 时,
时,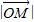 最小.
最小.点评:本题考查直线与椭圆的方程,考查向量知识,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
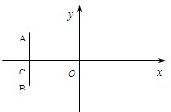 如图,在直角坐标系中,O为坐标原点,直线AB⊥x轴与点C,
如图,在直角坐标系中,O为坐标原点,直线AB⊥x轴与点C,