题目内容
在直角坐标系中,O为坐标原点,已知动圆与直线x=-1相切,且过定点F(1,0),动圆圆心为M.(1)求点M的轨迹C的方程;
(2)若过点F(1,0)的直线L与曲线C交于A,B两点,又点Q(-1,0),求△(3)QAB面积的最小值.
分析:(1)由题意知:|MN|=|MF|,根据抛物线的定义得,M的轨迹为以F为焦点的抛物线,且 p=2,从而写出抛物线的方程.
(2)当L的斜率不存在时,求出三角形QAB面积,当L的斜率存在时,用点斜式设出L的方程代入抛物线方程,依据根与系数的关系、弦长公式求出|AB|值,Q到L的距离d,代入三角形QAB面积公式并使用基本不等式求出它的最小值.
(2)当L的斜率不存在时,求出三角形QAB面积,当L的斜率存在时,用点斜式设出L的方程代入抛物线方程,依据根与系数的关系、弦长公式求出|AB|值,Q到L的距离d,代入三角形QAB面积公式并使用基本不等式求出它的最小值.
解答: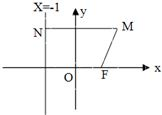 解:(1)由题意知:|MN|=|MF|,根据抛物线的定义得,M的轨迹为以F为焦点的抛物线,且 p=2,所以M的轨迹C的方程为y2=4x.
解:(1)由题意知:|MN|=|MF|,根据抛物线的定义得,M的轨迹为以F为焦点的抛物线,且 p=2,所以M的轨迹C的方程为y2=4x.
(2)当L的斜率不存在时,L:x=1,?A(1,2),B(1,-2),?s△QAB=
|AB||QF|=4
当L的斜率存在时,可设为K(K≠0),则L:y=K(x-1),与抛物线联立得
?x2-(2+
)x+1=0,设A(x1,y1),B(x2,y2),则|AB|=
=
,又Q到L的距离d=
,?s△QAB=
d|AB|=
=4
>4,所以,三角形QAB面积的最小值为4.
 解:(1)由题意知:|MN|=|MF|,根据抛物线的定义得,M的轨迹为以F为焦点的抛物线,且 p=2,所以M的轨迹C的方程为y2=4x.
解:(1)由题意知:|MN|=|MF|,根据抛物线的定义得,M的轨迹为以F为焦点的抛物线,且 p=2,所以M的轨迹C的方程为y2=4x.(2)当L的斜率不存在时,L:x=1,?A(1,2),B(1,-2),?s△QAB=
| 1 |
| 2 |
当L的斜率存在时,可设为K(K≠0),则L:y=K(x-1),与抛物线联立得
|
| 4 |
| K2 |
| (1+K2)[(x1+x2)2-4x1x2] |
| 4(1+K2) |
| K2 |
| 2|K| | ||
|
| 1 |
| 2 |
4
| ||
| |K| |
1+
|
点评:本题考查抛物线的定义、标准方程,点到直线的距离公式、弦长公式的应用,求出|AB|值是解题的关键和难点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
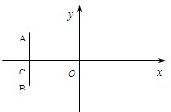 如图,在直角坐标系中,O为坐标原点,直线AB⊥x轴与点C,
如图,在直角坐标系中,O为坐标原点,直线AB⊥x轴与点C,