题目内容
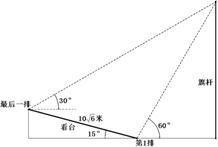
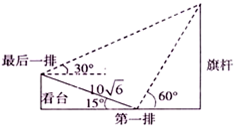 某校运动会开幕式上进行升旗仪式.如图,在坡度为15°的看台上,某一列座位与旗杆在同一个垂直于地面的平面上,在该列的第一排和最后一排测得旗杆顶端的仰角分别为60°和30°,且第一排和最后一排的距离为10
某校运动会开幕式上进行升旗仪式.如图,在坡度为15°的看台上,某一列座位与旗杆在同一个垂直于地面的平面上,在该列的第一排和最后一排测得旗杆顶端的仰角分别为60°和30°,且第一排和最后一排的距离为10| 6 |
30°
30°
.分析:根据题意可求得∠AEC和∠ACE,则∠EAC可求,然后利用正弦定理求得AC,最后在Rt△ABC中利用AB=AC•sin∠ACB求得AB的长,进而得到BC的长,即可求出所求角的正切进而求出结论.
解答: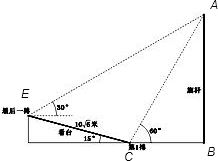 解:如图所示,依题意可知∠AEC=45°,
解:如图所示,依题意可知∠AEC=45°,
∠ACE=180°-60°-15°=105°
∴∠EAC=180°-45°-105°=30°
由正弦定理可知
=
CEsin∠EAC=ACsin∠CEA,
∴AC=
•sin∠CEA=20
米
∴在Rt△ABC中,
AB=AC•sin∠ACB=20
×
=30米
所以:旗杆的高度为30米.
故tan∠ACB=
⇒BC=30×
=10
.
设当国旗上升到离地面10米高时,在第一排测得国旗的仰角为θ,
∴tanθ=
=
.
解得:θ=30°.
故答案为:30°.
 解:如图所示,依题意可知∠AEC=45°,
解:如图所示,依题意可知∠AEC=45°,∠ACE=180°-60°-15°=105°
∴∠EAC=180°-45°-105°=30°
由正弦定理可知
| CE |
| sin∠EAC |
| AC |
| sin∠CEA |
∴AC=
| CE |
| sin∠EAC |
| 3 |
∴在Rt△ABC中,
AB=AC•sin∠ACB=20
| 3 |
| ||
| 2 |
所以:旗杆的高度为30米.
故tan∠ACB=
| AB |
| BC |
| ||
| 3 |
| 3 |
设当国旗上升到离地面10米高时,在第一排测得国旗的仰角为θ,
∴tanθ=
| 10 | ||
10
|
| ||
| 3 |
解得:θ=30°.
故答案为:30°.
点评:题主要考查了解三角形的实际应用.此类问题的解决关键是建立数学模型,把实际问题转化成数学问题,利用所学知识解决.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目
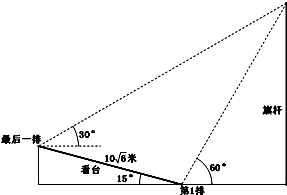 (2010•台州一模)某校运动会开幕式上举行升旗仪式,旗杆正好处在坡度15°的看台的某一列的正前方,从这一列的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°,且第一排和最后一排的距离为10
(2010•台州一模)某校运动会开幕式上举行升旗仪式,旗杆正好处在坡度15°的看台的某一列的正前方,从这一列的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°,且第一排和最后一排的距离为10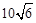 米(如图所示),旗杆底部与第一排在一个水平面上.若国歌长度约为50秒,升旗手应以_________(米/秒)的速度匀速升旗.
米(如图所示),旗杆底部与第一排在一个水平面上.若国歌长度约为50秒,升旗手应以_________(米/秒)的速度匀速升旗.
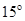
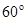 和
和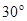 ,第一排和最后一排的距离
,第一排和最后一排的距离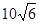 米(如图所示),旗杆底部与第一排在一个水平面上.
米(如图所示),旗杆底部与第一排在一个水平面上.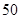 秒,升旗手应以
(米 /秒)的速度匀速升旗.
秒,升旗手应以
(米 /秒)的速度匀速升旗.