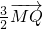题目内容
已知点H(0,-3),点P在x轴上,点Q在y轴正半轴上,点M在直线PQ上,且满足 .
.(I)当点P在x轴上移动时,求动点M的轨迹方程;
(Ⅱ)设动点M的轨迹为C,如果过定点A(x,y)的直线与曲线C相交不同的两点S、R,求证:曲线C在S、R两点处的切线的交点在一条定直线上.
【答案】分析:(I)设P(a,0),Q(0,b)(b>0),M(x,y).利用 ,即可得到a,b的关系,再利用
,即可得到a,b的关系,再利用 ,即可用x,y表示a,b,进而得到点M的轨迹方程.
,即可用x,y表示a,b,进而得到点M的轨迹方程.
(II)解法一:设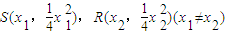 ,即得直线SR的方程,又A点在SR上,即可得到
,即得直线SR的方程,又A点在SR上,即可得到 ①
①
对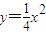 求导得:
求导得: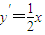 .即可得到抛物线上S、R处的切线方程,联立解得x,y代入①得即可.
.即可得到抛物线上S、R处的切线方程,联立解得x,y代入①得即可.
解法二:当过点A的直线斜率不存在时与题意不符.设直线SR的方程为y-y=k(x-x),与抛物线方程联立即可得到根与系数的关系.设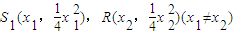 ,由过S,R点的切线方程联立可得交点的坐标,再利用根与系数的关系,即可得出.
,由过S,R点的切线方程联立可得交点的坐标,再利用根与系数的关系,即可得出.
解答:解:(I)设P(a,0),Q(0,b)(b>0),
∵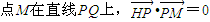 ,
,
∴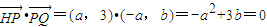 ,
,
∴a2=3b,
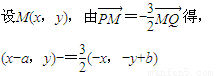
∴
∴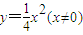
点M的轨迹方程为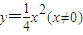 .
.
(II)解法一:设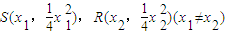 ,
,
则直线SR的方程为: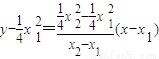
即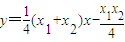 .
.
∵A点在SR上,
∴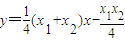 ①
①
对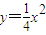 求导得:
求导得: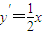 .
.
∴抛物线上S、R处的切线方程为: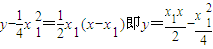 ②
②
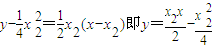 ③
③
联立②③,并解之得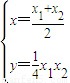 代入①得
代入①得
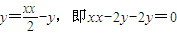 ,
,
故切线的交点在定直线xx-2y=2y=0上.
解法二:当过点A的直线斜率不存在时与题意不符.设直线SR的方程为y-y=k(x-x)
代入抛物线方程得x2-4kx+4xk-4y=0.
设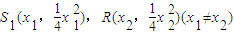
由韦达定理 (*)
(*)
又过S,R点的切线方程分别是:
∴ ,
,
代入(*)得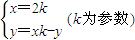 ,
,
消去k,得xx-2y-2y=0
故切线的交点在定直线xx-2y-2y=0上.
点评:熟练掌握向量的运算、直线与抛物线相交问题转化为方程联立得到根与系数的关系、导数的几何意义、切线方程等是解题的关键.
 ,即可得到a,b的关系,再利用
,即可得到a,b的关系,再利用 ,即可用x,y表示a,b,进而得到点M的轨迹方程.
,即可用x,y表示a,b,进而得到点M的轨迹方程.(II)解法一:设
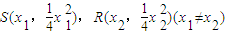 ,即得直线SR的方程,又A点在SR上,即可得到
,即得直线SR的方程,又A点在SR上,即可得到 ①
①对
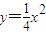 求导得:
求导得: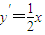 .即可得到抛物线上S、R处的切线方程,联立解得x,y代入①得即可.
.即可得到抛物线上S、R处的切线方程,联立解得x,y代入①得即可.解法二:当过点A的直线斜率不存在时与题意不符.设直线SR的方程为y-y=k(x-x),与抛物线方程联立即可得到根与系数的关系.设
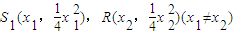 ,由过S,R点的切线方程联立可得交点的坐标,再利用根与系数的关系,即可得出.
,由过S,R点的切线方程联立可得交点的坐标,再利用根与系数的关系,即可得出.解答:解:(I)设P(a,0),Q(0,b)(b>0),
∵
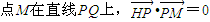 ,
,∴
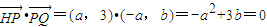 ,
,∴a2=3b,
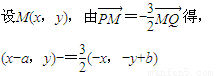
∴

∴
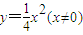
点M的轨迹方程为
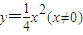 .
.(II)解法一:设
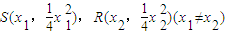 ,
,则直线SR的方程为:
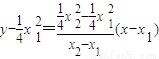
即
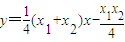 .
.∵A点在SR上,
∴
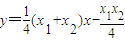 ①
①对
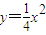 求导得:
求导得: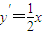 .
.∴抛物线上S、R处的切线方程为:
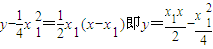 ②
②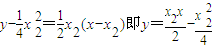 ③
③联立②③,并解之得
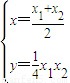 代入①得
代入①得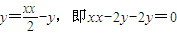 ,
,故切线的交点在定直线xx-2y=2y=0上.
解法二:当过点A的直线斜率不存在时与题意不符.设直线SR的方程为y-y=k(x-x)
代入抛物线方程得x2-4kx+4xk-4y=0.
设
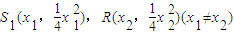
由韦达定理
 (*)
(*)又过S,R点的切线方程分别是:

∴
 ,
,代入(*)得
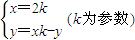 ,
,消去k,得xx-2y-2y=0
故切线的交点在定直线xx-2y-2y=0上.
点评:熟练掌握向量的运算、直线与抛物线相交问题转化为方程联立得到根与系数的关系、导数的几何意义、切线方程等是解题的关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
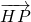 •
• =0,
=0,