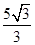题目内容
已知球的直径SC=4,A,B是该球球面上的两点,AB=2,∠ASC=∠BSC=60°,则棱锥S-ABC的体积为 .
分析:根据条件求出三棱锥的底面积和高的大小,利用三棱锥的体积公式即可求解.
解答:解:设球心为点O,∵为线段SC是球的直径,
∴它也是大圆的直径,
则得:∠SAC=∠SBC=90°,
∴在Rt△SAC中,SC=4,∠ASC=60° 得:AC=2
,SA=2,
又在Rt△SBC中,SC=4,∠BSC=,60° 得:BC=2
,SB=2,
∵AB=2,
∴△SAB为正三角形,△CAB为等腰三角形,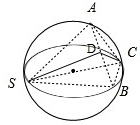
设AB的中点为D,连结SD和CD,
则SD=
,CD=
=
,
且SD⊥AB,CD⊥AB,
又SD∩CD=D,
∴AB⊥面SDC,
在△SCD中,SC=4,SD=
,CD=
,
∴由余弦定理得cos∠CSD=
=
=
,
即sin∠CSD=
=
=
=
,
△SCD的面积S=
SD•SC•sin∠CSD=
×
×4×
=2
,
棱锥S-ABC的体积:V=VA-SDC+VB-SDC=
S•AD+
S•BD=
S•AB=
AB•S△CSD=
×2×2
=
.
故答案为:
.
∴它也是大圆的直径,
则得:∠SAC=∠SBC=90°,
∴在Rt△SAC中,SC=4,∠ASC=60° 得:AC=2
| 3 |
又在Rt△SBC中,SC=4,∠BSC=,60° 得:BC=2
| 3 |
∵AB=2,
∴△SAB为正三角形,△CAB为等腰三角形,

设AB的中点为D,连结SD和CD,
则SD=
| 3 |
(2
|
| 11 |
且SD⊥AB,CD⊥AB,
又SD∩CD=D,
∴AB⊥面SDC,
在△SCD中,SC=4,SD=
| 3 |
| 11 |
∴由余弦定理得cos∠CSD=
| SC2+SD2-CD2 |
| 2SC•SD |
| 16+3-11 | ||
2×4×
|
| 1 | ||
|
即sin∠CSD=
1-(
|
1-
|
|
| ||
|
△SCD的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| ||
|
| 2 |
棱锥S-ABC的体积:V=VA-SDC+VB-SDC=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
4
| ||
| 3 |
故答案为:
4
| ||
| 3 |
点评:本题主要考查了球内接三棱锥的体积计算,利用利用分割法求锥体的体积,利用线面垂直的判定定理证明AB⊥面SCD是解决本题的关键,考查学生的运算能力,综合性较强,难度较大.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
已知球的直径SC=4,A,B是该球球面上的两点,AB=
,∠ASC=∠BSC=30°,则棱锥S-ABC的体积为( )
| 3 |
A、3
| ||
B、2
| ||
C、
| ||
| D、1 |
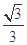 B.
B.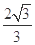 C.
C.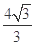 D.
D.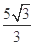
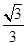 (B)
(B)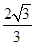
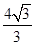 (D)
(D)