题目内容
如图,函数y=![]() |x|在x∈[-1,1]的图像上有两点A、B,AB∥Ox轴,点M(1,m)(m∈R且m>
|x|在x∈[-1,1]的图像上有两点A、B,AB∥Ox轴,点M(1,m)(m∈R且m>![]() )是△ABC的BC边的中点.
)是△ABC的BC边的中点.
(1)写出用B点横坐标t表示△ABC面积S的函数解析式S=f(t);
(2)求函数S=f(t)的最大值,并求出相应的C点坐标.

(1) f(t)=-3t2+2mt,t∈(0,1) (2) Smax=f(1)=2m-3,相应的C点坐标是(1,2m-3)
解析:
(1)依题意,设B(t,![]() t),A(-t,
t),A(-t, ![]() t)(t>0),C(x0,y0).
t)(t>0),C(x0,y0).
∵M是BC的中点![]() ∴
∴![]() =1,
=1,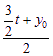 =m.
=m.
∴x0=2-t,y0=2m-![]() t.
t.
在△ABC中,|AB|=2t,AB边上的高hAB=y0-![]() t=2m-3t.
t=2m-3t.
∴S=![]() |AB|·hAB=
|AB|·hAB= ![]() ·2t·(2m-3t),即f(t)=-3t2+2mt,t∈(0,1).
·2t·(2m-3t),即f(t)=-3t2+2mt,t∈(0,1).
(2)∵S=-3t2+2mt=-3(t-![]() )2+
)2+![]() ,t∈(0,1
,t∈(0,1![]() ,若
,若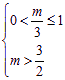 ,
,
即![]() <m≤3,
<m≤3,
当t=![]() 时,Smax=
时,Smax=![]() ,相应的C点坐标是(2-
,相应的C点坐标是(2-![]() ,
, ![]() m),
m),
若![]() >1,即m>3
>1,即m>3![]() S=f(t)在区间(0,1]上是增函数,
S=f(t)在区间(0,1]上是增函数,
∴Smax=f(1)=2m-3,相应的C点坐标是(1,2m-3).

练习册系列答案
相关题目
 如图是函数y=xα的图象,则α的取值可以是( )
如图是函数y=xα的图象,则α的取值可以是( ) |x|在x∈[-1,1]的图象上有两点A、B,AB∥
|x|在x∈[-1,1]的图象上有两点A、B,AB∥
 |x|在x∈[-1,1]的图象上有两点A,B,AB∥Ox轴,点M(1,m)(m是已知实数,且m>
|x|在x∈[-1,1]的图象上有两点A,B,AB∥Ox轴,点M(1,m)(m是已知实数,且m> )是△ABC的边BC的中点.
)是△ABC的边BC的中点.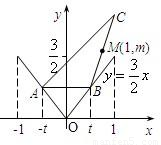
 ).
). ;②xy=9;③xy=
;②xy=9;③xy= .请确定哪个是等轴双曲线C的方程,并求出此双曲线的实轴长;
.请确定哪个是等轴双曲线C的方程,并求出此双曲线的实轴长; x+
x+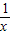 的图象也是双曲线,请尝试研究此双曲线的性质,你能得到哪些结论?(本小题将按所得到的双曲线性质的数量和质量酌情给分)
的图象也是双曲线,请尝试研究此双曲线的性质,你能得到哪些结论?(本小题将按所得到的双曲线性质的数量和质量酌情给分)