题目内容
已知等轴双曲线C的两个焦点F1、F2在直线y=x上,线段F1F2的中点是坐标原点,且双曲线经过点(3, ).
).(1)若已知下列所给的三个方程中有一个是等轴双曲线C的方程:①x2-y2=
 ;②xy=9;③xy=
;②xy=9;③xy= .请确定哪个是等轴双曲线C的方程,并求出此双曲线的实轴长;
.请确定哪个是等轴双曲线C的方程,并求出此双曲线的实轴长;(2)现要在等轴双曲线C上选一处P建一座码头,向A(3,3)、B(9,6)两地转运货物.经测算,从P到A、从P到B修建公路的费用都是每单位长度a万元,则码头应建在何处,才能使修建两条公路的总费用最低?
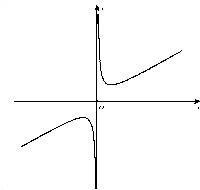
(3)如图,函数y=
 x+
x+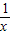 的图象也是双曲线,请尝试研究此双曲线的性质,你能得到哪些结论?(本小题将按所得到的双曲线性质的数量和质量酌情给分)
的图象也是双曲线,请尝试研究此双曲线的性质,你能得到哪些结论?(本小题将按所得到的双曲线性质的数量和质量酌情给分)
【答案】分析:(1)判断3个方程中哪一个是等轴双曲线C的方程,依题意,其两个焦点F1、F2在直线y=x上,可以排除①;且双曲线经过点(3, ).可排除②;计算可以确定③符合,进而联立方程
).可排除②;计算可以确定③符合,进而联立方程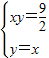 ,解得双曲线
,解得双曲线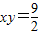 的两顶点坐标,即可得答案.
的两顶点坐标,即可得答案.
(2)根据题意,分析可将问题转化为在双曲线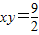 求一点P,使|PA|+|PB|最小,分析易得P位于第一象限,设双曲线的另一个焦点为F2其坐标为(-3,-3),由双曲线的定义可得PA|+|PB|=(|PF2|-6+|PB|),要求|PA|+|PB|的最小值,只需求|PF2|+|PB|的最小值,结合直线BF2的方程,易得答案.
求一点P,使|PA|+|PB|最小,分析易得P位于第一象限,设双曲线的另一个焦点为F2其坐标为(-3,-3),由双曲线的定义可得PA|+|PB|=(|PF2|-6+|PB|),要求|PA|+|PB|的最小值,只需求|PF2|+|PB|的最小值,结合直线BF2的方程,易得答案.
(3)类比双曲线的有关性质,分别求函数y=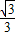 x+
x+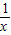 的图象的对称性等性质,分析出有关性质即可.
的图象的对称性等性质,分析出有关性质即可.
解答:解:(1)双曲线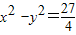 的焦点在x轴上,所以①不是双曲线c的方程
的焦点在x轴上,所以①不是双曲线c的方程
双曲线xy=9不经过点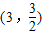 ,所以②不是双曲线C的方程
,所以②不是双曲线C的方程
所以③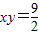 是等轴双曲线C的方程
是等轴双曲线C的方程
等轴双曲线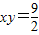 的焦点F1、F2在直线y=x上,
的焦点F1、F2在直线y=x上,
所以双曲线的顶点也在直线y=x上,
联立方程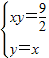 ,
,
解得双曲线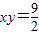 的两顶点坐标为(
的两顶点坐标为(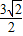 ,
,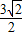 )(-
)(-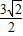 ,-
,-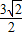 ),
),
所以双曲线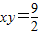 的实轴长为6
的实轴长为6
(2)所求问题即为:在双曲线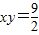 求一点P,使|PA|+|PB|最小.
求一点P,使|PA|+|PB|最小.
首先,点P应该选择在等轴双曲线的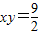 中第一象限的那一支上
中第一象限的那一支上
等轴双曲线的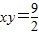 的长轴长为6,所以其焦距为
的长轴长为6,所以其焦距为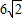
又因为双曲线的两个焦点F1、F2在直线y=x上,
线段F1F2的中点是原点,所以A(3,3)是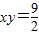 的一个焦点,
的一个焦点,
设双曲线的另一个焦点为F2(-3,-3),
由双曲线的定义知:|PA|=|PF2|-6
所以|PA|+|PB|=(|PF2|-6+|PB|),
要求|PA|+|PB|的最小值,只需求|PF2|+|PB|的最小值
直线BF2的方程为3x-4y-3=0,
所以直线BF2与双曲线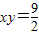 在第一象限的交点为
在第一象限的交点为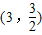
所以码头应在建点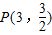 处,才能使修建两条公路的总费用最低
处,才能使修建两条公路的总费用最低
(3)①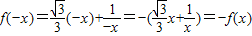 ,
,
此双曲线是中心对称图形,对称中心是原点(0,0);
②渐近线是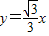 和x=0.当x>0时,
和x=0.当x>0时,
当x无限增大时,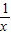 无限趋近于0,
无限趋近于0,
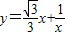 与
与 无限趋近;
无限趋近;
当y无限增大时,x无限趋近于0.
③双曲线的对称轴是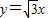 和
和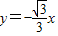 .
.
④实轴在直线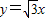 上,实轴长为
上,实轴长为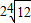
虚轴在直线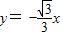 ,虚轴长为
,虚轴长为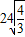
⑤焦点坐标为(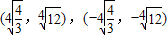 ),焦距
),焦距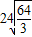 .
.
点评:本题难度较大,涉及双曲线的变形应用,解题时应紧扣双曲线的定义,找准焦点、顶点、实轴、虚轴的位置.
 ).可排除②;计算可以确定③符合,进而联立方程
).可排除②;计算可以确定③符合,进而联立方程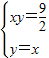 ,解得双曲线
,解得双曲线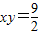 的两顶点坐标,即可得答案.
的两顶点坐标,即可得答案.(2)根据题意,分析可将问题转化为在双曲线
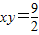 求一点P,使|PA|+|PB|最小,分析易得P位于第一象限,设双曲线的另一个焦点为F2其坐标为(-3,-3),由双曲线的定义可得PA|+|PB|=(|PF2|-6+|PB|),要求|PA|+|PB|的最小值,只需求|PF2|+|PB|的最小值,结合直线BF2的方程,易得答案.
求一点P,使|PA|+|PB|最小,分析易得P位于第一象限,设双曲线的另一个焦点为F2其坐标为(-3,-3),由双曲线的定义可得PA|+|PB|=(|PF2|-6+|PB|),要求|PA|+|PB|的最小值,只需求|PF2|+|PB|的最小值,结合直线BF2的方程,易得答案.(3)类比双曲线的有关性质,分别求函数y=
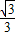 x+
x+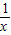 的图象的对称性等性质,分析出有关性质即可.
的图象的对称性等性质,分析出有关性质即可.解答:解:(1)双曲线
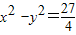 的焦点在x轴上,所以①不是双曲线c的方程
的焦点在x轴上,所以①不是双曲线c的方程双曲线xy=9不经过点
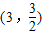 ,所以②不是双曲线C的方程
,所以②不是双曲线C的方程所以③
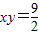 是等轴双曲线C的方程
是等轴双曲线C的方程等轴双曲线
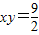 的焦点F1、F2在直线y=x上,
的焦点F1、F2在直线y=x上,所以双曲线的顶点也在直线y=x上,
联立方程
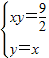 ,
,解得双曲线
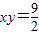 的两顶点坐标为(
的两顶点坐标为(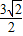 ,
,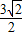 )(-
)(-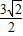 ,-
,-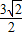 ),
),所以双曲线
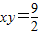 的实轴长为6
的实轴长为6(2)所求问题即为:在双曲线
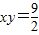 求一点P,使|PA|+|PB|最小.
求一点P,使|PA|+|PB|最小.首先,点P应该选择在等轴双曲线的
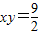 中第一象限的那一支上
中第一象限的那一支上等轴双曲线的
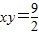 的长轴长为6,所以其焦距为
的长轴长为6,所以其焦距为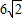
又因为双曲线的两个焦点F1、F2在直线y=x上,
线段F1F2的中点是原点,所以A(3,3)是
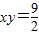 的一个焦点,
的一个焦点,设双曲线的另一个焦点为F2(-3,-3),
由双曲线的定义知:|PA|=|PF2|-6
所以|PA|+|PB|=(|PF2|-6+|PB|),
要求|PA|+|PB|的最小值,只需求|PF2|+|PB|的最小值
直线BF2的方程为3x-4y-3=0,
所以直线BF2与双曲线
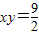 在第一象限的交点为
在第一象限的交点为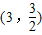
所以码头应在建点
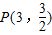 处,才能使修建两条公路的总费用最低
处,才能使修建两条公路的总费用最低(3)①
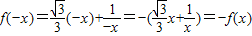 ,
,此双曲线是中心对称图形,对称中心是原点(0,0);
②渐近线是
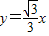 和x=0.当x>0时,
和x=0.当x>0时,当x无限增大时,
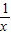 无限趋近于0,
无限趋近于0,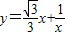 与
与 无限趋近;
无限趋近;当y无限增大时,x无限趋近于0.
③双曲线的对称轴是
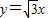 和
和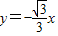 .
.④实轴在直线
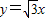 上,实轴长为
上,实轴长为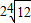
虚轴在直线
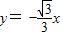 ,虚轴长为
,虚轴长为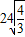
⑤焦点坐标为(
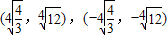 ),焦距
),焦距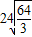 .
.点评:本题难度较大,涉及双曲线的变形应用,解题时应紧扣双曲线的定义,找准焦点、顶点、实轴、虚轴的位置.

练习册系列答案
相关题目
 已知等轴双曲线C的两个焦点F1、F2在直线y=x上,线段F1F2的中点是坐标原点,且双曲线经过点(3,
已知等轴双曲线C的两个焦点F1、F2在直线y=x上,线段F1F2的中点是坐标原点,且双曲线经过点(3,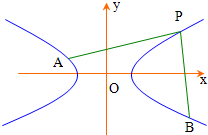 (2005•武汉模拟)已知等轴双曲线C:x2-y2=a2 (a>0)上一定点P(x0,y0)及曲线C上两动点AB满足(
(2005•武汉模拟)已知等轴双曲线C:x2-y2=a2 (a>0)上一定点P(x0,y0)及曲线C上两动点AB满足( ).
).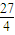 ;②xy=9;③xy=
;②xy=9;③xy= .请确定哪个是等轴双曲线C的方程,并求出此双曲线的实轴长;
.请确定哪个是等轴双曲线C的方程,并求出此双曲线的实轴长; x+
x+ 的图象也是双曲线,请尝试研究此双曲线的性质,你能得到哪些结论?(本小题将按所得到的双曲线性质的数量和质量酌情给分)
的图象也是双曲线,请尝试研究此双曲线的性质,你能得到哪些结论?(本小题将按所得到的双曲线性质的数量和质量酌情给分)
 ).
). ;②xy=9;③xy=
;②xy=9;③xy= .请确定哪个是等轴双曲线C的方程,并求出此双曲线的实轴长;
.请确定哪个是等轴双曲线C的方程,并求出此双曲线的实轴长;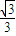 x+
x+ 的图象也是双曲线,请尝试研究此双曲线的性质,你能得到哪些结论?(本小题将按所得到的双曲线性质的数量和质量酌情给分)
的图象也是双曲线,请尝试研究此双曲线的性质,你能得到哪些结论?(本小题将按所得到的双曲线性质的数量和质量酌情给分)