题目内容
函数f(x)=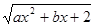 的定义域为
的定义域为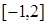 ,则该函数的值域为_________.
,则该函数的值域为_________.
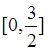
解析试题分析:根据题意可知函数f(x)=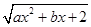 的定义域为
的定义域为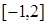 ,则说明了
,则说明了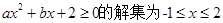 ,结合韦达定理得到-
,结合韦达定理得到-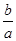 =1,
=1,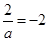 ,a=-1,b=1,可知函数的解析式为
,a=-1,b=1,可知函数的解析式为
f(x)=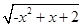 ,结合二次函数的性质可知,开口向下,对称轴为x =
,结合二次函数的性质可知,开口向下,对称轴为x =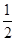 ,那么在定义域内先增后减,可知函数的最大值为当x=
,那么在定义域内先增后减,可知函数的最大值为当x=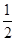 时,得到为
时,得到为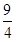 ,开平方后得到为
,开平方后得到为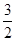 ,当x=-2时,函数值最小为0,因此可知道函数的 值域为
,当x=-2时,函数值最小为0,因此可知道函数的 值域为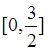 ,答案为
,答案为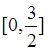 。
。
考点:本题主要是考查函数的定义域和值域的求解的运用。
点评:解决该试题的关键是利用函数的定义域和函数的单调性得到函数的值域问题同时也考察了一元二次不等式的逆用问题。

练习册系列答案
相关题目
 的定义域是____________.
的定义域是____________.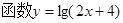 的定义域是
的定义域是 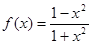 ,则
,则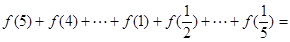 .
.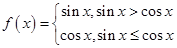 ,关于
,关于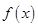 的叙述
的叙述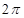 ②有最大值1和最小值
②有最大值1和最小值
 上单调递减
上单调递减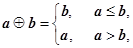 已知函数
已知函数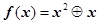 ,则
,则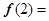 .
.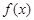 ,
, 满足
满足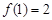 ,
,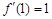 ,
,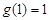 ,
,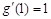 ,则函数
,则函数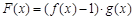 的图象在
的图象在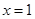 处的切线方程为 .
处的切线方程为 .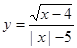 的定义域是 。
的定义域是 。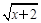 -
-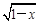 的值域是 .
的值域是 .