题目内容
在△ABC中,给出下列四个结论:
(1)若sin2A=sin2B,则△ABC是等腰三角形;
(2)若sinA=sinB,则△ABC是等腰三角形;
(3)若
=
=c,则△ABC是直角三角形;
(4)若sinA>sinB,则A>B.
其中正确命题的序号是 .
(1)若sin2A=sin2B,则△ABC是等腰三角形;
(2)若sinA=sinB,则△ABC是等腰三角形;
(3)若
| a |
| sinA |
| b |
| sinB |
(4)若sinA>sinB,则A>B.
其中正确命题的序号是
分析:(1)△ABC中,sin2A=sin2B⇒A=B或2A=π-2B,从而可判断其正误;
(2)利用正弦定理将角的正弦化“边”可判断(2);
(3)由正弦定理可知sinC=1,从而可判断(3)之正误;
(4)由正弦定理知sinA=
,sinB=
,从而可判断(4)之正误
(2)利用正弦定理将角的正弦化“边”可判断(2);
(3)由正弦定理可知sinC=1,从而可判断(3)之正误;
(4)由正弦定理知sinA=
| a |
| 2R |
| b |
| 2R |
解答:解:(1)△ABC中,∵sin2A=sin2B,
∴2A=2B或2A=π-2B,即A=B或A+B=
,
∴△ABC是等腰三角形或是直角三角形,故(1)错误;
(2)△ABC中,∵sinA=sinB,
由正弦定理知,sinA=
,sinB=
,
∴a=b,
∴△ABC是等腰三角形,故(2)正确;
(3)∵
=
=
=c,
∴sinC=1,
∴C=
,
∴△ABC是直角三角形,故(3)正确;
(4)由正弦定理知sinA=
,sinB=
,
∴sinA>sinB?
>
?a>b,
在△ABC中,“大边”对“大角”,
∴A>B,故(4)正确;
综上所述,正确命题的序号是(2)(3)(4).
故答案为:(2)(3)(4).
∴2A=2B或2A=π-2B,即A=B或A+B=
| π |
| 2 |
∴△ABC是等腰三角形或是直角三角形,故(1)错误;
(2)△ABC中,∵sinA=sinB,
由正弦定理知,sinA=
| a |
| 2R |
| b |
| 2R |
∴a=b,
∴△ABC是等腰三角形,故(2)正确;
(3)∵
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
∴sinC=1,
∴C=
| π |
| 2 |
∴△ABC是直角三角形,故(3)正确;
(4)由正弦定理知sinA=
| a |
| 2R |
| b |
| 2R |
∴sinA>sinB?
| a |
| 2R |
| b |
| 2R |
在△ABC中,“大边”对“大角”,
∴A>B,故(4)正确;
综上所述,正确命题的序号是(2)(3)(4).
故答案为:(2)(3)(4).
点评:本题考查正弦定理的应用,考查诱导公式及特殊角的三角函数值,突出转化思想的考查,属于中档题.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
在△ABC中,B(-2,0),C(2,0),A(x,y),给出△ABC满足的条件,就能得到动点A的轨迹方程,下表给出了一些条件及方程:
则满足条件①、②、③的轨迹方程分别为 (用代号C1、C2、C3填入).
则满足条件①、②、③的轨迹方程分别为
| 条 件 | 方 程 | ||||
| ①△ABC的周长为10 | C1:y2=25 | ||||
| ②△ABC的面积为10 | C2:x2+y2=4(y≠0) | ||||
| ③△ABC中,∠A=90° | C3:
|
在△ABC中,B(-2,0),C(2,0),A(x,y),给出△ABC满足的条件,就能得到动点A的轨迹方程,下表给出了一些条件及方程:
|
| A、C3、C1、C2 |
| B、C2、C1、C3 |
| C、C1、C3、C2 |
| D、C3、C2、C1 |
在△ABC中,A(x,y),B(-2,0),C(2,0),给出△ABC满足的条件,就能得到动点A的轨迹方程,下表给出了一些条件及方程:
则满足条件①、②、③的轨迹方程分别用代号表示为( )
A.E3,E1,E2
B.E1,E2,E3
C.E3,E2,E1
D.E1,E3,E2
| 条件 | 方程 |
| ①△ABC周长为10; ②△ABC面积为10; ③△ABC中,∠A=90° | E1:y2=25; E2:x2+y2=4(y≠0); E3: 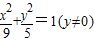 |
A.E3,E1,E2
B.E1,E2,E3
C.E3,E2,E1
D.E1,E3,E2
在△ABC中,B(-2,0),C(2,0),A(x,y),给出△ABC满足的条件,就能得到动点A的轨迹方程,下表给出了一些条件及方程:
则满足条件①、②、③的轨迹方程分别为 (用代号C1、C2、C3填入).
则满足条件①、②、③的轨迹方程分别为 (用代号C1、C2、C3填入).
| 条 件 | 方 程 |
| ①△ABC的周长为10 | C1:y2=25 |
| ②△ABC的面积为10 | C2:x2+y2=4(y≠0) |
| ③△ABC中,∠A=90° | C3: |