题目内容
在△ABC中,A(x,y),B(-2,0),C(2,0),给出△ABC满足的条件,就能得到动点A的轨迹方程,下表给出了一些条件及方程:| 条件 | 方程 |
| ①△ABC周长为10; ②△ABC面积为10; ③△ABC中,∠A=90° | E1:y2=25; E2:x2+y2=4(y≠0); E3: 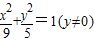 |
A.E3,E1,E2
B.E1,E2,E3
C.E3,E2,E1
D.E1,E3,E2
【答案】分析:根据题意,依次分析可得,①中可转化为A点到B、C两点距离之和为常数,符合椭圆的定义,利用定义法求轨迹方程;②中利用三角形面积公式可知A点到BC距离为常数,轨迹为两条直线;③中∠A=90°,可用斜率或向量处理.
解答:解:①△ABC的周长为10,即AB+AC+BC=10,而BC=4,所以AB+AC=6>BC,故动点A的轨迹为椭圆,与E3对应;
②△ABC的面积为10,所以 BC•|y|=10,|y|=5,与E1对应,
BC•|y|=10,|y|=5,与E1对应,
③∠A=90°,故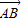 •
• =(-2-x,-y)(2-x,-y)=x2+y2-4=0,与E2对应.
=(-2-x,-y)(2-x,-y)=x2+y2-4=0,与E2对应.
故满足条件①、②、③的轨迹方程分别用代号表示为E3E1E2
故选A.
点评:本题考查直接法、定义法求轨迹方程,属基本题型、基本方法的考查.
解答:解:①△ABC的周长为10,即AB+AC+BC=10,而BC=4,所以AB+AC=6>BC,故动点A的轨迹为椭圆,与E3对应;
②△ABC的面积为10,所以
 BC•|y|=10,|y|=5,与E1对应,
BC•|y|=10,|y|=5,与E1对应,③∠A=90°,故
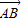 •
• =(-2-x,-y)(2-x,-y)=x2+y2-4=0,与E2对应.
=(-2-x,-y)(2-x,-y)=x2+y2-4=0,与E2对应.故满足条件①、②、③的轨迹方程分别用代号表示为E3E1E2
故选A.
点评:本题考查直接法、定义法求轨迹方程,属基本题型、基本方法的考查.

练习册系列答案
相关题目
下面是一道选择题的两种解法,两种解法看似都对,可结果并不一致,问题出在哪里
?在△ABC中,a=x,b=2,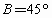 ,若△ABC有两解,则x的取值范围是
,若△ABC有两解,则x的取值范围是
[
]|
A .(2,+∞) |
B .(0,2) |
C .(2,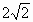 ) ) |
D .(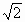 ,2) ,2) |
解法
1 △ABC有两解,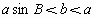 ,
,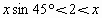 ,
,
即
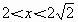 ,故选C.
,故选C.
解法
2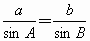 ,
,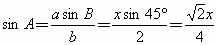 .
.
△
ABC有两解,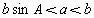 ,
,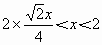 ,即0<x<2,故选B.
,即0<x<2,故选B.