题目内容
已知△ABC三边a,b,c的长都是整数,且a≤b≤c,如果b=25,则符合条件的三角形共有( )个.A.124
B.225
C.300
D.325
【答案】分析:根据题意,a可取的值为1、2、3、…25,由三角形的三边关系,有25≤c<25+a,对a分情况讨论,分析可得c可取的情况,即可得这种情况下符合条件的三角形的个数,由分类计数原理,结合等差数列的前n项和公式,计算可得答案.
解答:解:根据题意,a可取的值为1、2、3、…25,
根据三角形的三边关系,有25≤c<25+a,
当a=1时,有25≤c<26,则c=25,有1种情况,
当a=2时,有25≤c<27,则c=25、26,有2种情况,
当a=3时,有25≤c<28,则c=25、26、27,有3种情况,
当a=4时,有25≤c<29,则c=25、26、27、28,有4种情况,
…
当a=25时,有有25≤c<50,则c=25、26、27、28…49,有25种情况,
则符合条件的三角形共有1+2+3+4+…+25=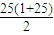 =325;
=325;
故选D.
点评:本题考查合情推理与分类计数原理的运用,涉及三角形三边的关系,关键是发现a变化时,符合条件的三角形个数的变化规律.
解答:解:根据题意,a可取的值为1、2、3、…25,
根据三角形的三边关系,有25≤c<25+a,
当a=1时,有25≤c<26,则c=25,有1种情况,
当a=2时,有25≤c<27,则c=25、26,有2种情况,
当a=3时,有25≤c<28,则c=25、26、27,有3种情况,
当a=4时,有25≤c<29,则c=25、26、27、28,有4种情况,
…
当a=25时,有有25≤c<50,则c=25、26、27、28…49,有25种情况,
则符合条件的三角形共有1+2+3+4+…+25=
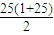 =325;
=325;故选D.
点评:本题考查合情推理与分类计数原理的运用,涉及三角形三边的关系,关键是发现a变化时,符合条件的三角形个数的变化规律.

练习册系列答案
相关题目