题目内容
(理)函数y=f(x)图象与h(x)=-x2+6x-8图象关于点(1,0)对称.
①求f(x)的表达式;
②设g(x)=f(x)-2x+|x+1-a|(a∈R),求g(x)的最小值.
①求f(x)的表达式;
②设g(x)=f(x)-2x+|x+1-a|(a∈R),求g(x)的最小值.
分析:①设(x,y)是y=f(x)上任意一点,q求出其关于(1,0)的对称点,将对称点的坐标代入h(x)=-x2+6x-8的解析式即得到f(x)的解析式.
②通过对x的讨论将g(x)的解析式中的绝对值去掉,画出相应的图象,通过对a的分类讨论求出g(x)的最小值.
②通过对x的讨论将g(x)的解析式中的绝对值去掉,画出相应的图象,通过对a的分类讨论求出g(x)的最小值.
解答:解:①设(x,y)是y=f(x)上任意一点,则其关于(1,0)的对称点为(2-x,-y),
因为函数y=f(x)图象与h(x)=-x2+6x-8图象关于点(1,0)对称,
所以点(2-x,-y)应该在h(x)=-x2+6x-8的图象上,
所以-y=-(2-x)2+6(2-x)-8,
整理得y=x 2+2x,
所以f(x)=x2+2x,
②g(x)=f(x)-2x+|x+1-a|
=x2+|x+1-a|
=

结合图象,
当a-1≤-
时即a≤
时,
当x=-
时,函数g(x)有最小值
-a
当a-1≥
时即a≥
时,
当x=
时,函数g(x)有最小值为a-
;
当
<a<
时,当x=a-1时函数g(x)有最小值(a-1)2
总之,g(x)的最小值为
因为函数y=f(x)图象与h(x)=-x2+6x-8图象关于点(1,0)对称,
所以点(2-x,-y)应该在h(x)=-x2+6x-8的图象上,
所以-y=-(2-x)2+6(2-x)-8,
整理得y=x 2+2x,
所以f(x)=x2+2x,
②g(x)=f(x)-2x+|x+1-a|
=x2+|x+1-a|
=
|

结合图象,
当a-1≤-
| 1 |
| 2 |
| 1 |
| 2 |
当x=-
| 1 |
| 2 |
| 3 |
| 4 |
当a-1≥
| 1 |
| 2 |
| 3 |
| 2 |
当x=
| 1 |
| 2 |
| 5 |
| 4 |
当
| 1 |
| 2 |
| 3 |
| 2 |
总之,g(x)的最小值为
|
点评:本题考查根据函数的性质求函数的解析式、求二次函数的最值应该先求出二次函数的对称轴、考查分类讨论的数学思想方法,是一道较难的题目.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
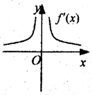
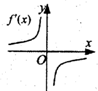
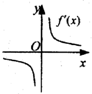
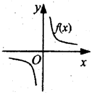
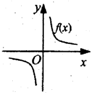 (理)函数y=f(x)的图象如图所示,则导函数y=f′(x)的图象大致是( )
(理)函数y=f(x)的图象如图所示,则导函数y=f′(x)的图象大致是( )