Question

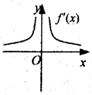
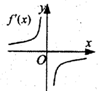
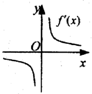
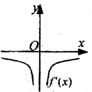
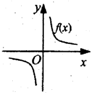
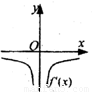
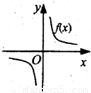
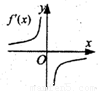
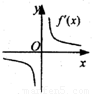
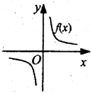（理）函数y=f（x）的图象如图所示，则导函数y=f′（x）的图象大致是（　　）

A．

B．

C．

D．

Answer 1

分析：先根据函数y=f（x）的图象可知函数在区间（-∞，0），（0，+∞）上都是单调减函数，可知导函数y=f'（x）在区间（-∞，0），（0，+∞）上的值小于0，然后得出它的导函数的性质即可直接判断．

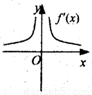
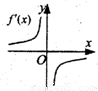
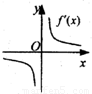
解答：解：由f（x）的图象及f′（x）的意义知，在x＞0时，f′（x）为单调递增函数且f′（x）＜0；在x＜0时，
f′（x）为单调递减函数且f′（x）＜0．故选D

点评：本题考查学生灵活运用导数知识与观察问题的能力．考查导函数与原函数之间的关系，应主要导函数看正负，原函数看增减．