Question

已知函数f(x)=(x-1)²,g(x)=4(x-1),数列{a_n}满足a₁=2,a_n≠1,(a_n+1-a_n)g(a_n)+f(a_n)=0.

（Ⅰ）求证：a_n+1=a_n+;

（Ⅱ）证明：数列{a_n-1}为等比数列，并求{a_n}的通项公式.

Answer 1

证明：（Ⅰ）由已知f(a_n)=(a_n-1)²,g(a_n)=4(a_n-1),

∵(a_n+1-a_n)g(a_n)+f(a_n)=0.∴(a_n+1-a_n)4(a_n-1)+(a_n-1)²=0,∴即3-2a_n-4a_n+1a_n+4a_n+1-1=0

(-1)+(2-2a_n)-4a_n+1(a_n-1)=0，即(a_n-1)(3a_n-4a_n+1+1)=0,

∵a_n≠1,∴3a_n-4a_n+1+1=0,∴a_a+1=(3a_n+1)=a_n+.

（Ⅱ）证明：=,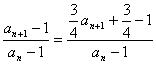

∴{a_n-1}是以a₁-1=0为首项，公比为的等比数列，∴a_n-1=()^n-1,∴a_n=()^n-1+1.