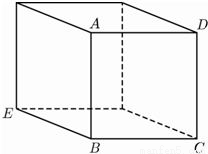
题目内容

空间中一长方体如下图所示，其中ABCD为正方形，
.
BE
为长方体的一边．已知cot∠AEB=
2
6
5
，则cot∠CED=
 

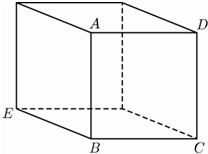
精英家教网
分析：如图，先根据图形得到，∠ABE=∠DCE=90°，再在直角三角形中利用边角关系得到
.
AB
=
.
BC
=
.
CD
=
.
DA
=acot∠AEB，
通过解直角形即可求得cot∠CED的值．
解答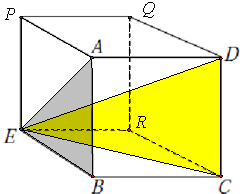：精英家教网解：如图，∠ABE=∠DCE=90°
设
.
AB
=
.
BC
=
.
CD
=
.
DA
=acot∠AEB=
2
6
5
?
.
BE
a
=
2
6
5

?
.
BE
=
2
6
5
a
.
CE
=
.
BC
2+
.
BE
2
=
a2+(
2
6
5
a)2
=
7
5
a
故cot∠CED=
.
CE
.
CD
=
7
5
a
a
=
7
5

故答案为：
7
5
点评：本题主要考查了棱柱的结构特征，解答的关键是利用直角三角形的边角之间的关系求解．
练习册系列答案
相关题目
空间中一长方体如下图所示，其中ABCD为正方形，
.
BE
为长方体的一边．已知cot∠AEB=
2
6
5
，则cot∠CED=______

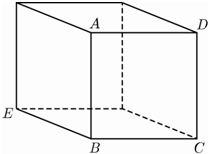
精英家教网
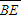空间中一长方体如下图所示，其中ABCD为正方形，为长方体的一边．已知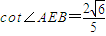，则cot∠CED=   

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网