题目内容
已知偶函数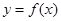 在区间
在区间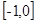 上是增函数,且满足
上是增函数,且满足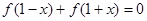 ,下列判断中错误的是( )
,下列判断中错误的是( )
A.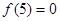
B.函数 在
在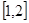 上单调递减
上单调递减
C.函数 的图像关于直线
的图像关于直线 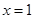 对称
对称
D.函数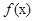 的周期是
的周期是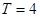
A
【解析】
试题分析:对于A,令x=0代入题中等式,得f(1-0)+f(1+0)=0,∴f(1)=0,结合函数为偶函数得f(-1)=f(1)=0,再令x=2代入题中等式,,得f(1-2)+f(1+2)=0,得f(3)=-f(-1)=0,结合函数为偶函数得f(-3)=f(3)=0,最后令x=4,f(1-4)+f(1+4)=0,得f(5)=-f(-3)=0,故A项正确;对于B,因为偶函数y=f(x)图象关于y轴对称,在区间[-1,0]上是增函数,所以y=f(x)在区间[0,1]上是减函数,设F(x)=f(1+x),得F(-x)=f(1-x),因为f(1-x)+f(1+x)=0,得f(1+x)=-f(1-x),所以F(x)=f(1+x)是奇函数,图象关于原点对称.由此可得y=f(x)图象关于点(1,0)对称.∵区间[1,2]和区间[0,1]是关于点(1,0)对称的区间,且在对称的区间上函数的单调性一致,∴函数f(x)在[1,2]上单调递减,故B项正确;对于C,由B项的证明可知,y=f(x)图象关于点(1,0)对称,若f(x)的图象同时关于直线 x=1对称,则f(x)=0恒成立,这样与“在区间[-1,0]上f(x)是增函数”矛盾,故C不正确;对于D,因为f(x)=f(1-(1-x))=-f(1+(1+x))=-f(x+2),所以f(x+2)=-f(x+4),可得f(x+4)=f(x),函数f(x)的周期是T=4,D项正确,故选C
考点:本题考查了函数的性质
点评:给出抽象函数,要我们在给出的几条性质中找出错误的一项,着重考查了抽象函数的性质和函数单调性、奇偶性等知识,属于中档题

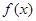 在区间
在区间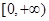 上是增函数,如果
上是增函数,如果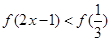 ,则
,则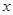 的取值范围是( )
的取值范围是( )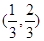 B.
B. C.
C.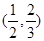 D.
D.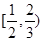
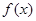 在区间
在区间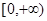 上单调递增,则满足不等式
上单调递增,则满足不等式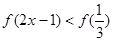 的
的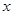 的取值范围是 ( )
的取值范围是 ( )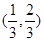 B.
B.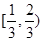 C.
C.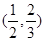 D.
D.
 在区间
在区间 上是增函数,下列不等式一定成立的是
上是增函数,下列不等式一定成立的是
 B.
B.

 D.
D.

 在区间
在区间 上是增函数,下列不等式一定成立的是( )
上是增函数,下列不等式一定成立的是( ) B.
B.
 D.
D.