题目内容
若关于x的不等式(组)0≤x2+
x-
<
对任意n∈N*恒成立,则所有这样的解x的集合是
| 7 |
| 9 |
| 2n |
| (2n+1)2 |
| 2 |
| 9 |
{-1,
}
| 2 |
| 9 |
{-1,
}
.| 2 |
| 9 |
分析:将
的分子分母同除2n,结合“对勾函数“的单调性,求出
=
∈(0,
],进而将恒成立问题转化为最值问题后,可得x2+
x-
=0,解方程可得答案.
| 2n |
| (2n+1)2 |
| 2n |
| (2n+1)2 |
| 1 | ||
(2n+
|
| 2 |
| 9 |
| 7 |
| 9 |
| 2 |
| 9 |
解答:解:若0≤x2+
x-
<
对任意n∈N*恒成立,
即
-
≤x2+
x-
<
对任意n∈N*恒成立,
∵
=
∈(0,
]
故0≤x2+
x-
≤0
即x2+
x-
=0
解得x=-1或x=-
故所有这样的解x的集合是{-1,
}
故答案为:{-1,
}
| 7 |
| 9 |
| 2n |
| (2n+1)2 |
| 2 |
| 9 |
即
| 2n |
| (2n+1)2 |
| 2 |
| 9 |
| 7 |
| 9 |
| 2 |
| 9 |
| 2n |
| (2n+1)2 |
∵
| 2n |
| (2n+1)2 |
| 1 | ||
(2n+
|
| 2 |
| 9 |
故0≤x2+
| 7 |
| 9 |
| 2 |
| 9 |
即x2+
| 7 |
| 9 |
| 2 |
| 9 |
解得x=-1或x=-
| 2 |
| 9 |
故所有这样的解x的集合是{-1,
| 2 |
| 9 |
故答案为:{-1,
| 2 |
| 9 |
点评:本题考查的知识点是函数恒成立问题,基本不等式,其中将恒成立问题转化为最值问题是解答此类问题的关键.

练习册系列答案
相关题目
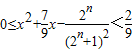 对任意n∈N*恒成立,则所有这样的解x的集合是 .
对任意n∈N*恒成立,则所有这样的解x的集合是 .