题目内容
在一次射击比赛中,8个泥制的靶子挂成三列(如图),其中有两列各挂3个,一列挂2个,一位射手按照下列规则去击碎靶子:先挑选一列,然后必须击碎这列中尚未击碎的靶子中最低一个,若每次射击都严格执行这一规则,击碎全部8个靶子的不同方法有
| A.560 | B.320 | C.650 | D.360 |
A
解析试题分析:根据已知条件,那么根据游戏的规则,先挑选一列,然后必须击碎这列中尚未击碎的靶子中最低一个,那么可知对于其中的几个靶子是有顺序的,先确定最下面的击中的情况有 ,Z再从剩下的当中选出两个位置就是一,三列的第二个击中的情况,有
,Z再从剩下的当中选出两个位置就是一,三列的第二个击中的情况,有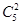 ,其余的就位移确定了,那么利用分步乘法计数原理得到共有560个。选A.
,其余的就位移确定了,那么利用分步乘法计数原理得到共有560个。选A.
考点:本试题考查了排列组合的运用。
点评:解决该试题的关键是利用已知条件确定好了击碎8个靶子的所有情况,在这个过程中,一个环节要注意,也就是说第一,三列的下面两个球被击中是有先后顺序的,那么可知,结合定序排列问题来得到结论。属于中档题。

练习册系列答案
相关题目
从 台甲型和
台甲型和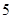 台乙型电视机中任意取出
台乙型电视机中任意取出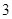 台,其中至少有甲型与乙型电视机各
台,其中至少有甲型与乙型电视机各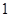 台,则不同的取法共有( )
台,则不同的取法共有( )
A.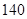 种 种 | B.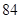 种 种 | C. 种 种 | D.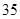 种 种 |
将4个不同的球放入3个不同的盒中,每个盒内至少有1个球,则不同的放法种数为( )
| A.24 | B.36 | C.48 | D.96 |
某台小型晚会由6个节目组成,演出顺序有如下要求:节目甲必须排在第四位、节目乙不能排在第一位,节目丙不能排在最后一位,该台晚会节目演出顺序的编排方案共有
| A.36种 | B.42种 | C.48种 | D.54种 |
 展开式中的常数项是
展开式中的常数项是
A. | B. | C. | D. |
 且
且 ,则乘积
,则乘积 等于
等于
A. | B. | C. | D. |
已知 的展开式中
的展开式中 的系数为30,则正实数
的系数为30,则正实数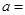 ( )
( )
A. | B. | C. | D. |
 种,选出三人班级委的选法共有
种,选出三人班级委的选法共有 种,则
种,则 是 ( )
是 ( )



 是
是 (n≥2且n∈N)的展开式中x的一次项的系数,则
(n≥2且n∈N)的展开式中x的一次项的系数,则 的值为( )
的值为( )