题目内容
某台小型晚会由6个节目组成,演出顺序有如下要求:节目甲必须排在第四位、节目乙不能排在第一位,节目丙不能排在最后一位,该台晚会节目演出顺序的编排方案共有
| A.36种 | B.42种 | C.48种 | D.54种 |
B
解析试题分析:因为节目甲必须排在第四位,所以可以不再考虑节目甲,又因为节目乙不能排在第一位,节目丙不能排在最后一位,所以如果节目乙排在最后一位,则有 种排法;如果节目乙也不排在最后一位,则最后一位还有三个节目可选,所以有
种排法;如果节目乙也不排在最后一位,则最后一位还有三个节目可选,所以有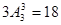 种排法,所以共有42种排法.
种排法,所以共有42种排法.
考点:本小题主要考查排列的应用.
点评:应用排列组合知识解决有限制条件的实际问题时,要注意采用特殊元素优先、特殊位置优先等方法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设(x-b)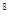 =b
=b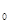 +b
+b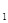 x+b
x+b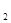 x
x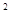 +…+b
+…+b x
x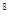 ,如果b
,如果b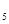 +b
+b =-6,则实数b的值为
=-6,则实数b的值为
A.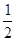 | B.-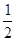 | C.2 | D.-2 |
二项式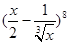 的展开式中常数项是
的展开式中常数项是
| A.28 | B.-7 | C.7 | D.-28 |
设复数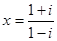 (
(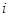 是虚数单位),则
是虚数单位),则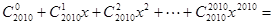 ( )
( )
A.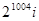 | B.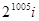 | C.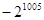 | D.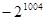 |
在一次射击比赛中,8个泥制的靶子挂成三列(如图),其中有两列各挂3个,一列挂2个,一位射手按照下列规则去击碎靶子:先挑选一列,然后必须击碎这列中尚未击碎的靶子中最低一个,若每次射击都严格执行这一规则,击碎全部8个靶子的不同方法有
| A.560 | B.320 | C.650 | D.360 |
设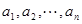 是1,2,…,
是1,2,…,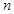 的一个排列,把排在
的一个排列,把排在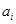 的左边且比
的左边且比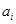 小的数的个数称为
小的数的个数称为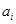 的顺序数(
的顺序数( )。如:在排列
)。如:在排列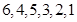 中,5的顺序数为1,3的顺序数为0。则在1至8这八个数字构成的全排列中,同时满足8的顺序数为2,7的顺序数为3,5的顺序数为3的不同排列种数为( )
中,5的顺序数为1,3的顺序数为0。则在1至8这八个数字构成的全排列中,同时满足8的顺序数为2,7的顺序数为3,5的顺序数为3的不同排列种数为( )
| A.48 | B.96 | C.144 | D.192 |
从10名大学生村官中选3个人担任乡长助理,则甲、丙至少有1人人选,而乙没有人选的不同选法的种数位为
| A. 85 | B. 56 | C. 49 | D. 28 |
 B.
B.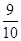 C.
C.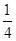 D.
D.