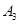题目内容
在一个有奖问答的电视节目中,参赛选手顺序回答A1、A2、A3三个问题,答对各个问题所获奖金(单位:元)对应如下表:
当一个问题回答正确后,选手可选择继续回答下一个问题,也可选择放弃.若选择放弃,选手将获得答对问题的累计奖金,答题结束;若有任何一个问题回答错误,则全部奖金归零,答题结束.设一名选手能正确回答A1、A2、A3的概率分别为
、
、
,正确回答一个问题后,选择继续回答下一个问题的概率均为
,且各个问题回答正确与否互不影响.
(Ⅰ)按照答题规则,求该选手回答到A2且回答错误的概率;
(Ⅱ)求该选手所获奖金数为0的概率.
| A1 | A2 | A3 |
| 1000 | 2000 | 3000 |
| 4 |
| 5 |
| 2 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2 |
(Ⅰ)按照答题规则,求该选手回答到A2且回答错误的概率;
(Ⅱ)求该选手所获奖金数为0的概率.
分析:(Ⅰ)由题意可得,该选手回答到A2且回答错误的概率为
×
×
,运算求得结果.
(Ⅱ)先求出①回答A1错误的概率、②回答A1正确但回答A2错误的概率、③回答A1、A2正确但回答A3错误的概率,相加,即得所求.
| 4 |
| 5 |
| 1 |
| 2 |
|
(Ⅱ)先求出①回答A1错误的概率、②回答A1正确但回答A2错误的概率、③回答A1、A2正确但回答A3错误的概率,相加,即得所求.
解答:解:(Ⅰ)该选手回答到A2且回答错误的概率为:P=
×
×
=
.…(6分)
(Ⅱ)该选手所获奖金为0包含三种情况:
①回答A1错误,其概率为P1=1-
=
;
②回答A1正确但回答A2错误,其概率为P2=
×
×
=
;
③回答A1、A2正确但回答A3错误,其概率为P3=
×
×
×
×
=
;
∴该选手所获奖金数为0的概率为P1+P2+P3=
.…(12分)
| 4 |
| 5 |
| 1 |
| 2 |
|
| 2 |
| 15 |
(Ⅱ)该选手所获奖金为0包含三种情况:
①回答A1错误,其概率为P1=1-
| 4 |
| 5 |
| 1 |
| 5 |
②回答A1正确但回答A2错误,其概率为P2=
| 4 |
| 5 |
| 1 |
| 2 |
|
| 2 |
| 15 |
③回答A1、A2正确但回答A3错误,其概率为P3=
| 4 |
| 5 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
|
| 1 |
| 10 |
∴该选手所获奖金数为0的概率为P1+P2+P3=
| 13 |
| 30 |
点评:本题主要考查等可能事件的概率,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在一个有奖问答的电视节目中,参赛选手顺序回答 三个问题,答对各个问题所获奖金(单位:元)对应如下表:
三个问题,答对各个问题所获奖金(单位:元)对应如下表:
|
|
|
|
|
|
|
|
当一个问题回答正确后,选手可选择继续回答下一个问题,也可选择放弃.若选择放弃,选手将获得答对问题的累计奖金,答题结束;若有任何一个问题回答错误,则全部奖金归零,答题结束.设一名选手能正确回答 的概率分别为
的概率分别为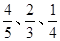 ,正确回答一个问题后,选择继续回答下一个问题的概率均为
,正确回答一个问题后,选择继续回答下一个问题的概率均为 ,且各个问题回答正确与否互不影响.
,且各个问题回答正确与否互不影响.
(Ⅰ)按照答题规则,求该选手 回答正确但所得奖金为零的概率;
回答正确但所得奖金为零的概率;
(Ⅱ)设该选手所获奖金总数为 ,求
,求 的分布列与数学期望.
的分布列与数学期望.
| 在一个有奖问答的电视节目中,参赛选手顺序回答A1、A2、A3三个问题,答对各个问题所获奖金(单位:元)对应如下表: | ||||||
 ,正确回答一个问题后,选择继续回答下一个问题的概率均为 ,正确回答一个问题后,选择继续回答下一个问题的概率均为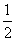 ,且各个问题回答正确与否互不影响。 ,且各个问题回答正确与否互不影响。 | ||||||
| (1)按照答题规则,求该选手A1回答正确但所得奖金为零的概率; (2)设该选手所获奖金总数为ξ,求ξ的分布列与数学期望。 |
(本小题满分12分)
在一个有奖问答的电视节目中,参赛选手顺序回答三个问题,答对各个问题所获奖金(单位:元)对应如下表:
当一个问题回答正确后,选手可选择继续回答下一个问题,也可选择放弃.若选择放弃,选手将获得答对问题的累计奖金,答题结束;若有任何一个问题回答错误,则全部奖金归零,答题结束.设一名选手能正确回答的概率分别为,正确回答一个问题后,选择继续回答下一个问题的概率均为,且各个问题回答正确与否互不影响.
(Ⅰ)按照答题规则,求该选手回答正确但所得奖金为零的概率;
(Ⅱ)设该选手所获奖金总数为,求的分布列与数学期望.