题目内容
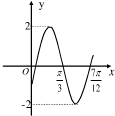 如图为三角函数f(x)=Asin(ωx+φ)(A>0,ω>0,
如图为三角函数f(x)=Asin(ωx+φ)(A>0,ω>0,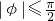 )图象的一段.
)图象的一段.
(1)求函数的解析式及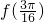 的值;
的值;
(2)如果函数y=f (x)-m在(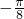 ,
,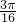 )内有且仅有一个零点,求实数m的取值范围.
)内有且仅有一个零点,求实数m的取值范围.
解:(1)由题意与图象可知A=2,T=2×(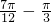 )=
)= ,所以ω=
,所以ω= =4.
=4.
曲线经过( )所以0=2sin(4×
)所以0=2sin(4× +φ),
+φ),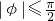 ,
,
φ=- ,
,
三角函数f(x)=2sin(4x ).
).
f(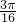 )=2sin(4×
)=2sin(4×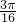
 )=2sin
)=2sin cos
cos -2cos
-2cos sin
sin =
= .
.
(2)x∈(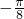 ,
,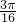 ),所以
),所以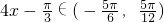 ,
,
函数y=f (x)-m在(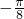 ,
,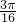 )内有且仅有一个零点,
)内有且仅有一个零点,
即方程2sin(4x )=m在(
)=m在(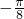 ,
,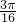 )内有且仅有一个根,
)内有且仅有一个根,
所以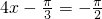 ,函数只有一个零点,此时m=-2;
,函数只有一个零点,此时m=-2;
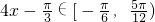 时函数也只有一个零点,此时-1≤m<
时函数也只有一个零点,此时-1≤m< .
.
分析:(1)通过函数的图象,求出A,T得到ω,利用图象经过( ),求出φ即可得到函数的解析式,然后利用两角差的正弦函数求出
),求出φ即可得到函数的解析式,然后利用两角差的正弦函数求出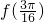 的值;
的值;
(2)函数y=f (x)-m在(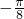 ,
,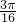 )内有且仅有一个零点,转化方程只有一个根,即可求实数m的取值范围.
)内有且仅有一个零点,转化方程只有一个根,即可求实数m的取值范围.
点评:本题考查函数解析式的求法,函数的零点与方程的根,考查分析问题解决问题的能力,转化思想的应用.
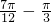 )=
)= ,所以ω=
,所以ω= =4.
=4.曲线经过(
 )所以0=2sin(4×
)所以0=2sin(4× +φ),
+φ),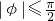 ,
,φ=-
 ,
,三角函数f(x)=2sin(4x
 ).
).f(
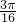 )=2sin(4×
)=2sin(4×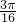
 )=2sin
)=2sin cos
cos -2cos
-2cos sin
sin =
= .
.(2)x∈(
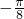 ,
,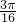 ),所以
),所以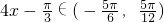 ,
,函数y=f (x)-m在(
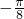 ,
,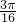 )内有且仅有一个零点,
)内有且仅有一个零点,即方程2sin(4x
 )=m在(
)=m在(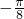 ,
,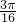 )内有且仅有一个根,
)内有且仅有一个根,所以
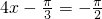 ,函数只有一个零点,此时m=-2;
,函数只有一个零点,此时m=-2;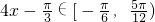 时函数也只有一个零点,此时-1≤m<
时函数也只有一个零点,此时-1≤m< .
.分析:(1)通过函数的图象,求出A,T得到ω,利用图象经过(
 ),求出φ即可得到函数的解析式,然后利用两角差的正弦函数求出
),求出φ即可得到函数的解析式,然后利用两角差的正弦函数求出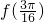 的值;
的值;(2)函数y=f (x)-m在(
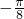 ,
,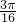 )内有且仅有一个零点,转化方程只有一个根,即可求实数m的取值范围.
)内有且仅有一个零点,转化方程只有一个根,即可求实数m的取值范围.点评:本题考查函数解析式的求法,函数的零点与方程的根,考查分析问题解决问题的能力,转化思想的应用.

练习册系列答案
相关题目
 如图为三角函数f(x)=Asin(ωx+φ)(A>0,ω>0,
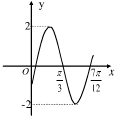
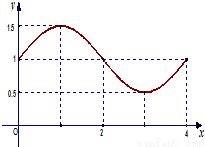
如图为三角函数f(x)=Asin(ωx+φ)(A>0,ω>0,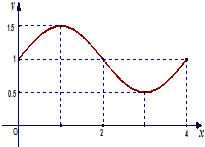 若三角函数f(x)的部分图象如图,则函数f(x)的解析式,以及S=f(1)+f(2)+…+f(2012)的值分别为( )
若三角函数f(x)的部分图象如图,则函数f(x)的解析式,以及S=f(1)+f(2)+…+f(2012)的值分别为( )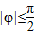 )图象的一段.
)图象的一段.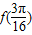 的值;
的值;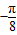 ,
,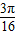 )内有且仅有一个零点,求实数m的取值范围.
)内有且仅有一个零点,求实数m的取值范围.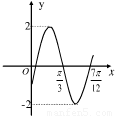
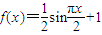 ,S=2012
,S=2012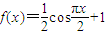 ,S=2012
,S=2012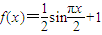 ,S=2012.5
,S=2012.5 ,S=2012.5
,S=2012.5