题目内容
．某几何体的三视图如图所示，该几何体的体积为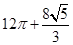
，则其正视图中x的值为
| A．5 | B．4 | C．3 | D．2 |
C
解析考点：由三视图求面积、体积．
分析：几何体是一个组合体，上面是一个正四棱锥，四棱锥的底面是一个对角线为4的正方形，侧棱长是3，下面是一个圆柱，底面直径是4，母线长是x，写出几何体的体积，得到关于x的方程，解出结果．
：由三视图知，几何体是一个组合体，
上面是一个正四棱锥，四棱锥的底面是一个对角线为4的正方形，
侧棱长是3，根据直角三角形勾股定理知圆锥的高是
=
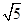
下面是一个圆柱，底面直径是4，母线长是x，
∵几何体的体积为，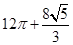
∴π×4x+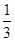
×(2
)2×=，
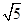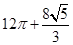∴x=3，
故答案为：3
练习册系列答案
相关题目
已知一个长方体的同一顶点处的三条棱长分别为1，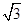
，2，则其外接球的表面积为
A． | B． | C． | D． |
平面A1B1C1，正视图是边长为2的正方形，俯视图为一个等边三角形，该三棱柱的左视图的面积为 （ ）
如下图所示，甲、乙、丙是三个立体图形的三视图，甲、乙、丙对应的标号正确的是( )
①长方体 ②圆锥 ③三棱锥 ④圆柱
| A．④③② | B．②①③ | C．①②③ | D．③②④ |
的侧面
内有一动点
到直线
与直线
的距离相等,则动点
棱柱的侧棱
| A．相交于一点 | B．平行但不相等 |
| C．平行且相等 | D．可能平行也可能相交于一点 |
在平面上，若两个正三角形的边长比
为1:2.则它们的面积之比为1:4.类似地，在空间中，若两个正四面体的棱长比为1:2，则它们
的体积比为（ ）
| A．1:2 | B．1:4 | C．1:6 | D．1:8 |
圆柱的底面直径与高都等于某个球的直径，则该球的表
面积与圆柱全面积的比是
A． | B． | C． | D． |
与球
有且只有一个公共点
，从直线
截球的两截面圆的半径分别为
和
，二面角
的平面角为
，则球
