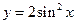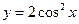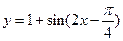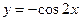题目内容
(本小题满分13分)
设函数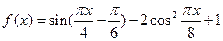 .
.
(Ⅰ)求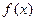 的最小正周期.
的最小正周期.
(Ⅱ)若函数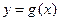 与
与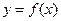 的图像关于直线
的图像关于直线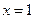 对称,求当
对称,求当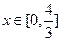 时
时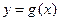 的最大值.
的最大值.
设函数
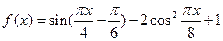 .
.(Ⅰ)求
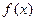 的最小正周期.
的最小正周期. (Ⅱ)若函数
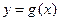 与
与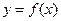 的图像关于直线
的图像关于直线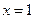 对称,求当
对称,求当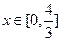 时
时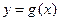 的最大值.
的最大值.(Ⅰ)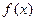 的最小正周期为T =
的最小正周期为T = 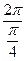 =8
=8
(Ⅱ)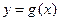 在
在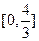 上的最大值为
上的最大值为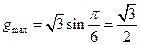
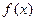 的最小正周期为T =
的最小正周期为T = 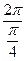 =8
=8(Ⅱ)
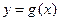 在
在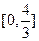 上的最大值为
上的最大值为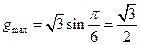
解:(Ⅰ)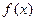 =
=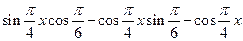 =
=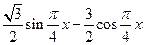
=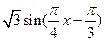 ……………5分
……………5分
故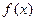 的最小正周期为T =
的最小正周期为T = 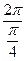 =8………………6分
=8………………6分
(Ⅱ)解法一:在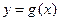 的图象上任取一点
的图象上任取一点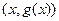 ,它关于
,它关于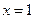 的对称点
的对称点 . 由题设条件,点
. 由题设条件,点 在
在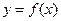 的图象上,从而
的图象上,从而
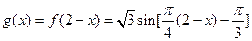 =
=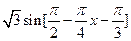
=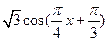 ……………10分
……………10分
当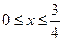 时,
时,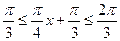 ,因此
,因此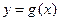 在区间
在区间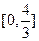 上的最大值为
上的最大值为
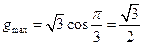 ……………………13分
……………………13分
解法二:因区间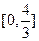 关于x = 1的对称区间为
关于x = 1的对称区间为 ,且
,且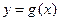 与
与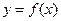 的图象关于x = 1对称,故
的图象关于x = 1对称,故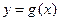 在
在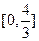 上的最大值为
上的最大值为
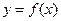 在
在 上的最大值……………………10分
上的最大值……………………10分
由(Ⅰ)知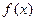 =
=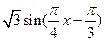 ,当
,当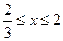 时,
时,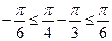
因此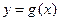 在
在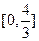 上的最大值为
上的最大值为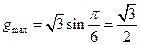 ……………………13分
……………………13分
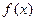 =
=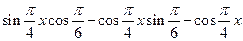 =
=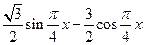
=
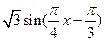 ……………5分
……………5分故
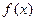 的最小正周期为T =
的最小正周期为T = 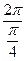 =8………………6分
=8………………6分(Ⅱ)解法一:在
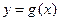 的图象上任取一点
的图象上任取一点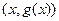 ,它关于
,它关于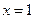 的对称点
的对称点 . 由题设条件,点
. 由题设条件,点 在
在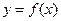 的图象上,从而
的图象上,从而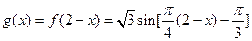 =
=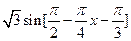
=
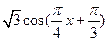 ……………10分
……………10分当
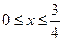 时,
时,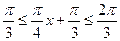 ,因此
,因此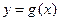 在区间
在区间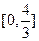 上的最大值为
上的最大值为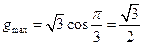 ……………………13分
……………………13分解法二:因区间
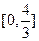 关于x = 1的对称区间为
关于x = 1的对称区间为 ,且
,且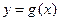 与
与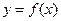 的图象关于x = 1对称,故
的图象关于x = 1对称,故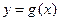 在
在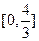 上的最大值为
上的最大值为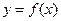 在
在 上的最大值……………………10分
上的最大值……………………10分由(Ⅰ)知
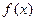 =
=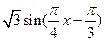 ,当
,当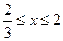 时,
时,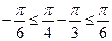
因此
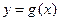 在
在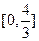 上的最大值为
上的最大值为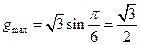 ……………………13分
……………………13分
练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
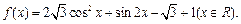 求:
求: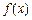 的最小正周期;
的最小正周期;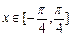 时,求
时,求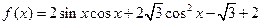
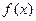 的对称轴方程;
的对称轴方程;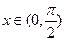 时,若函数
时,若函数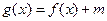 有零点,求m的范围;
有零点,求m的范围;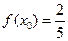 ,
,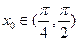 ,求
,求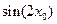 的值.
的值. 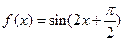 ,在下列四个命题中:
,在下列四个命题中: 的最小正周期是
的最小正周期是 ;
; 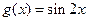 的图像向左平移
的图像向左平移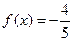 ,
,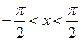 ,则
,则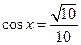
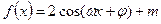 ,对任意实数
,对任意实数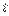 都
都 有
有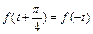 ,且
,且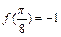 ,则实数
,则实数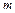 的
的 值等于 ( )
值等于 ( )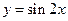 的图象向左平移
的图象向左平移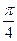 个单位长度,向上平移1个单位长度,所得图象对应的函数解析式是( )
个单位长度,向上平移1个单位长度,所得图象对应的函数解析式是( )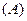
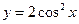
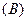
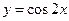
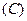

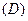
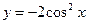
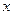 是三角形的最小内角,则函数
是三角形的最小内角,则函数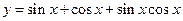 的最大值是( )
的最大值是( )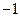
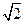
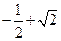
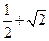
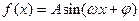 (其中A>0,
(其中A>0,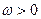 ,
,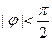 )的图象如图所示,则,f(0)= 。
)的图象如图所示,则,f(0)= 。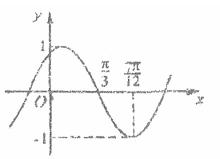
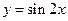 的图象向右平移
的图象向右平移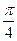 个单位,向上平移
个单位,向上平移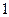 个单位,所得图象的函数解析式是
个单位,所得图象的函数解析式是