题目内容
设直线![]()
![]() 与抛物线
与抛物线![]() 所围成的图形面积为S,它们与直线
所围成的图形面积为S,它们与直线![]() 围成的面积为T, 若U=S+T达到最小值,求
围成的面积为T, 若U=S+T达到最小值,求![]() 值.
值.
解析:
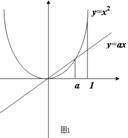
首先做草图,求得直线![]()
![]() 与抛物线
与抛物线![]() 的交点.用定积分求面积
的交点.用定积分求面积![]() 和
和 ![]() (关于
(关于![]() 的函数).进而用导数研究函数的单调性,并求最值.
的函数).进而用导数研究函数的单调性,并求最值.
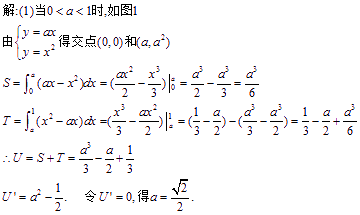
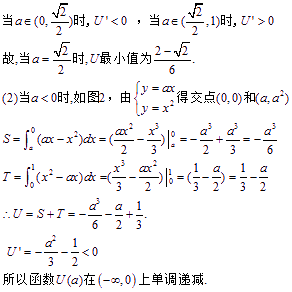
故函数![]() 无最小值。
无最小值。
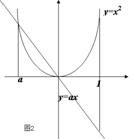
当![]() 时,显然无最小值。
时,显然无最小值。
讲评:结合解析几何的知识,考察定积分求曲边梯形的面积,同时结合导数研究函数的单调性和最值.

练习册系列答案
相关题目
题目内容
设直线![]()
![]() 与抛物线
与抛物线![]() 所围成的图形面积为S,它们与直线
所围成的图形面积为S,它们与直线![]() 围成的面积为T, 若U=S+T达到最小值,求
围成的面积为T, 若U=S+T达到最小值,求![]() 值.
值.
首先做草图,求得直线![]()
![]() 与抛物线
与抛物线![]() 的交点.用定积分求面积
的交点.用定积分求面积![]() 和
和 ![]() (关于
(关于![]() 的函数).进而用导数研究函数的单调性,并求最值.
的函数).进而用导数研究函数的单调性,并求最值.
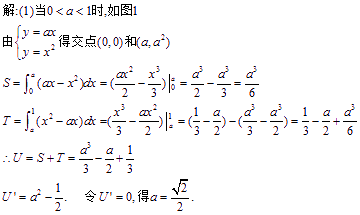
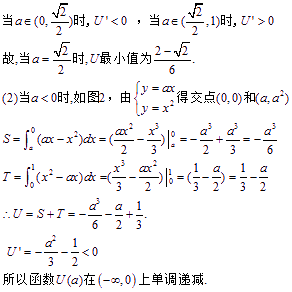


故函数![]() 无最小值。
无最小值。
当![]() 时,显然无最小值。
时,显然无最小值。
讲评:结合解析几何的知识,考察定积分求曲边梯形的面积,同时结合导数研究函数的单调性和最值.
