题目内容
已知抛物线![]()
![]() 经过点A(2,1),过A作倾斜角互补的两条不同直线
经过点A(2,1),过A作倾斜角互补的两条不同直线![]() .
.
(Ⅰ)求抛物线![]() 的方程及准线方程;
的方程及准线方程;
(Ⅱ)当直线![]() 与抛物线
与抛物线![]() 相切时,求直线
相切时,求直线![]() 与抛物线
与抛物线![]() 所围成封闭区域的面积;
所围成封闭区域的面积;
(Ⅲ)设直线![]() 分别交抛物线
分别交抛物线![]() 于B,C两点(均不与A重合),若以线段BC为直径的圆与抛物线的准线相切,求直线BC的方程.
于B,C两点(均不与A重合),若以线段BC为直径的圆与抛物线的准线相切,求直线BC的方程.
同下
解析:
(Ⅰ)由于A(2,1)在抛物线![]() 上, 所以
上, 所以 ![]() ,即
,即![]() . …….2分
. …….2分
故所求抛物线的方程为![]() ,其准线方程为
,其准线方程为![]() . ………….3分
. ………….3分
(Ⅱ)当直线![]() 与抛物线相切时,由
与抛物线相切时,由![]() ,可知直线
,可知直线![]() 的斜率为1,其倾斜角为
的斜率为1,其倾斜角为![]() ,所以直线
,所以直线![]() 的倾斜角为
的倾斜角为![]() ,故直线
,故直线![]() 的斜率为
的斜率为![]() ,所以
,所以![]() 的方程为
的方程为![]() …….4分
…….4分
将其代入抛物线的方程![]() ,
, 得
得 ![]() , 解得
, 解得 ![]() , …….5分
, …….5分
所以直线![]() 与抛物线所围成封闭区域的面积为:
与抛物线所围成封闭区域的面积为:
![]() ……………….6分
……………….6分
![]()
![]() ……………….8分
……………….8分
(Ⅲ)不妨设直线AB的方程为![]() , ……………….9分
, ……………….9分
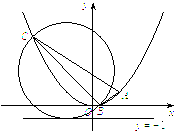 由
由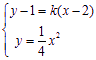
得![]() , ……………….10分
, ……………….10分
易知该方程有一个根为2,所以另一个根为![]() ,
,
所以点B的坐标为![]() ,
,
同理可得C点坐标为![]() , ……………….11分
, ……………….11分
所以![]()
![]()
![]() , ……………….12分
, ……………….12分
线段BC的中点为![]() ,因为以BC为直径的圆与准线
,因为以BC为直径的圆与准线![]() 相切,
相切,
所以 ![]() ,由于
,由于![]() , 解得
, 解得 ![]() . …………….13分
. …………….13分
此时,点B的坐标为![]() ,点C的坐标为
,点C的坐标为![]() ,
,
直线BC的斜率为![]() ,
,
所以,BC的方程为![]() ,即
,即![]() . …….14分
. …….14分

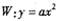 经过点A(2,1),过A作倾斜角互补的两条不同直线
经过点A(2,1),过A作倾斜角互补的两条不同直线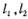 .
.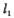 与抛物线W相切时,求直线
与抛物线W相切时,求直线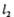 的方程;
的方程;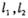 分别交抛物线W于B、C两点(均不与4重合),若以线段BC为直径的圆与抛物线的准线相切,求直线BC的方程.
分别交抛物线W于B、C两点(均不与4重合),若以线段BC为直径的圆与抛物线的准线相切,求直线BC的方程.