题目内容
(12分)已知函数f(x)=lnx-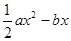 (a≠0)
(a≠0)
(1)若a=3,b=-2,求f(x)在[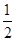 ,e]的最大值;
,e]的最大值;
(2)若b=2,f(x)存在单调递减区间,求a的范围.
【答案】
(1)当且仅当x=1,f(x)max=f(1)= a-b=-
a-b=-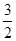 +2=
+2= ;
;
(2) a的范围(-1,0)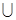 (0,+
(0,+ )
)
【解析】本试题主要是考查了导数在研究函数中的运用。求解函数的最值和函数单调性的逆向运用。
(1)由于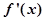 =
=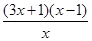 ,然后分析当a=3,b=-2,时的导数,分别为正和负的取值范围,得到单调性,然后求解极值,和最值。
,然后分析当a=3,b=-2,时的导数,分别为正和负的取值范围,得到单调性,然后求解极值,和最值。
(2)因为f(x)存在递减区间, f′(x)<0有解那么即等价于ax2+2x-1>0有x>0的解,利用对参数a讨论得到范围。
f′(x)<0有解那么即等价于ax2+2x-1>0有x>0的解,利用对参数a讨论得到范围。
解:(1)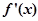 =
=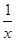 -ax-b=
-ax-b=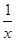 -3x+2=
-3x+2=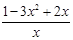 =-
=-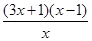
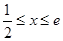 当
当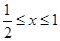 时 f′(x)
时 f′(x)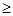 0; 1<x
0; 1<x e
f′(x)<0
e
f′(x)<0
当且仅当x=1,f(x)max=f(1)= a-b=-
a-b=-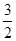 +2=
+2= ……5分
……5分
(2) 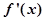 =
= 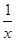 -ax-2=
-ax-2=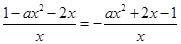
f(x)存在递减区间, f′(x)<0有解
f′(x)<0有解
ax2+2x-1>0有x>0的解…………7分
a>0,显然满足…………9分
a<0时,则△=4+4a>0且ax2+2x-1=0至少有一个正根,此时-1<a<0……11分
 a的范围(-1,0)
a的范围(-1,0)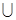 (0,+
(0,+ ) …………12分
) …………12分

练习册系列答案
相关题目







 x
x -ax+(a-1)
-ax+(a-1) ,
, 。讨论函数
。讨论函数 的单调性;
的单调性; 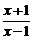 ,求函数φ (x)的单调区间;
,求函数φ (x)的单调区间;