题目内容
已知函数f(x)=msinx+ cosx(m>0)的最大值为2.
cosx(m>0)的最大值为2.
(1)求函数f(x)在[0,π]上的单调递减区间;(2)△ABC中, 角A,B,C所对的边分别是a,b,c, 且C=60°,c=3,求△ABC的面积.
角A,B,C所对的边分别是a,b,c, 且C=60°,c=3,求△ABC的面积.
(1)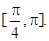 ; (2)
; (2) .
.
解析试题分析:(1)根据辅助角公式,函数的最大值为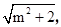 令其为2,即可求得m,利用正弦函数的单调性可求得此函数的递减区间,找到[0,π]上的单调递减区间即可;(2)本小题关键是求得边a与b的乘积,利用正弦定理,把
令其为2,即可求得m,利用正弦函数的单调性可求得此函数的递减区间,找到[0,π]上的单调递减区间即可;(2)本小题关键是求得边a与b的乘积,利用正弦定理,把 化为边a与b的关系,另一方面已知C=60°,c=3,由余弦定理,可得边a与b的另一关系,两式联立解得ab(当然也可解得a与b的单个值,但计算量大),利用
化为边a与b的关系,另一方面已知C=60°,c=3,由余弦定理,可得边a与b的另一关系,两式联立解得ab(当然也可解得a与b的单个值,但计算量大),利用 可求得面积.
可求得面积.
试题解析:(1)由题意,f(x)的最大值为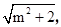 所以
所以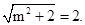 而m>0,于是m=
而m>0,于是m= ,f(x)=2sin(x+
,f(x)=2sin(x+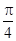 ).由正弦函数的单调性及周期性可得x满足
).由正弦函数的单调性及周期性可得x满足 即
即 所以f(x)在[0,π]上的单调递减区间为
所以f(x)在[0,π]上的单调递减区间为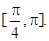
(2)设△ABC的外接圆半径为R,由题意,得 化简
化简 得sin A+sin B=2
得sin A+sin B=2 sin Asin B.由正弦定理,得
sin Asin B.由正弦定理,得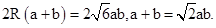 ① 由余弦定理,得a2+b2-ab=9,即(a+b)2-3ab-9="0." ②
① 由余弦定理,得a2+b2-ab=9,即(a+b)2-3ab-9="0." ②
将①式代入②,得2(ab)2-3ab-9=0,解得ab=3或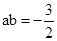 (舍去),故
(舍去),故
考点:辅助角公式, 正弦函数的单调性,正弦定理, 余弦定理,方程思想,三角形面积公式: .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
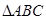 中,角
中,角 的对边分别为
的对边分别为 ,设S为△ABC的面积,满足4S=
,设S为△ABC的面积,满足4S=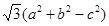 .
. 的大小;
的大小;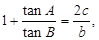 且
且 求
求 的值.
的值.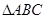 的内角
的内角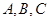 的对边分别
的对边分别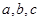 且
且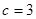 ,
,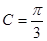 ,若
,若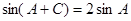 ,求
,求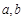 的值。
的值。 中,内角
中,内角 的对边分别为
的对边分别为 ,满足
,满足 .
. 的度数;
的度数;  求
求
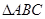 中,角
中,角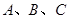 所对的边为
所对的边为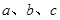 ,且满足
,且满足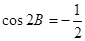 ,
,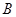 的值;(2)若
的值;(2)若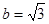 且
且 ,求
,求 的取值范围.
的取值范围. ≥0对一切实数
≥0对一切实数 恒成立.
恒成立. 为
为 的三个内角
的三个内角 的对边,
的对边, ,则
,则