题目内容
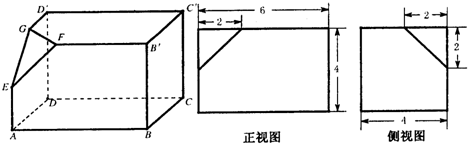
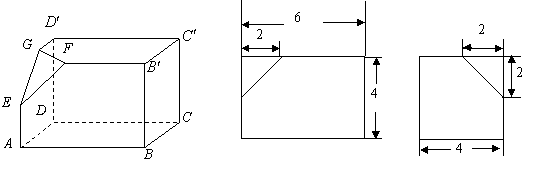
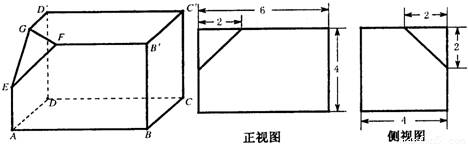
如下的三个图中,左面的是一个长方体截去一个角所得多面体的直观图,它的主视图和左视图在右面画出(单位:cm).(1)按照给出的尺寸,求该多面体的体积;(2)在所给直观图中连结BC′,证明:BC′∥面EFG.


分析:(1)按照给出的尺寸,利用切割法得V=V长方体-V正三棱锥,代入体积公式求该多面体的体积;
(2)在长方体ABCD-A′B′C′D′中,连接AD′,根据条件和长方体的几何特征证明EG∥BC′,再由线面平行的判定定理证明BC′∥面EFG.
(2)在长方体ABCD-A′B′C′D′中,连接AD′,根据条件和长方体的几何特征证明EG∥BC′,再由线面平行的判定定理证明BC′∥面EFG.
解答:解:(1)由题意可得:
所求多面体体积V=V长方体-V正三棱锥
=4×4×6-
×
×2×2×2=
(cm2),
(2)证明:如图,
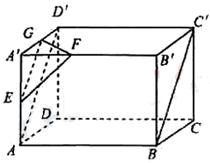 由多面体的左视图可得:点G、F分别是正方形的中点,
由多面体的左视图可得:点G、F分别是正方形的中点,
在长方体ABCD-A′B′C′D′中,连接AD′,
则AD′∥BC′
∵E,G分别为AA′,A′D′中点,
∴AD′∥EG,从而EG∥BC′,
又∵EG?平面EFG,BC′?平面EFG,
∴BC′∥平面EFG.
所求多面体体积V=V长方体-V正三棱锥
=4×4×6-
| 1 |
| 3 |
| 1 |
| 2 |
| 284 |
| 3 |
(2)证明:如图,
 由多面体的左视图可得:点G、F分别是正方形的中点,
由多面体的左视图可得:点G、F分别是正方形的中点,在长方体ABCD-A′B′C′D′中,连接AD′,
则AD′∥BC′
∵E,G分别为AA′,A′D′中点,
∴AD′∥EG,从而EG∥BC′,
又∵EG?平面EFG,BC′?平面EFG,
∴BC′∥平面EFG.
点评:本题主要考查由三视图求面积、体积,求解的关键是由视图得出几何体的长、宽、高等性质,各种类型的几何体求体积的公式;以及证明线面平行的判定定理以及证明过程.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目