题目内容
已知定义域为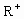 的函数f(x),对于任意x,y∈
的函数f(x),对于任意x,y∈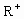 时,恒有
时,恒有
f(xy)=f(x)+f(y).
(Ⅰ)求证:当x∈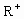 时,f(
时,f(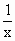 )=-f(x);
)=-f(x);
(Ⅱ)若x>1时,恒有f(x)<0,求证:f(x)必有反函数;
(Ⅲ)设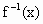 是f(x)的反函数,求证:
是f(x)的反函数,求证: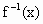 在其定义域内恒有
在其定义域内恒有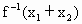 =
=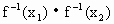 .
.
答案:
解析:
解析:
|
(Ⅰ)证明:令x=y=1, 则f(1)=f(1)+f(1), ∴f(1)=0 又令y= 则f(x)+ ∴ ∴当x∈ (Ⅱ)证明:设 则 故 ∴ ∴f(x)在定义域 因此,f(x)必有反函数. (Ⅲ)解:∵ ∴ 于是 ∴ |

练习册系列答案
相关题目
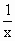 ,
,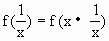 =f(1),
=f(1),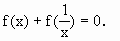
 时,f(
时,f(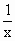 )=-f(x).
)=-f(x).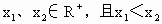 ,
,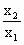 >1.
>1.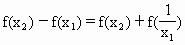
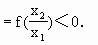
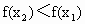 .
.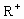 上是单调递减函数.
上是单调递减函数.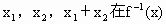 的定义域内,
的定义域内,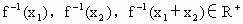 .
.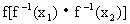
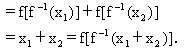
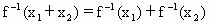 .
.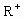 的函数f(x),对于任意x,y∈
的函数f(x),对于任意x,y∈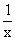 )=-f(x);
)=-f(x);