题目内容
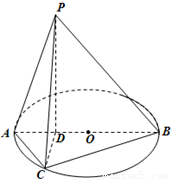 如图所示,已知AB为圆O的直径,点D为线段AB上一点,且AD=
如图所示,已知AB为圆O的直径,点D为线段AB上一点,且AD= DB,点C为圆O上一点,且BC=
DB,点C为圆O上一点,且BC=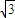 AC.点P在圆O所在平面上的正投影为点D,PD=DB.
AC.点P在圆O所在平面上的正投影为点D,PD=DB.(1)求证:PA⊥CD;
(2)求二面角C-PB-A的余弦值.
【答案】分析:(1)先利用平面几何知识与线面垂直的性质证线线垂直,由线线垂直⇒线面垂直,再由线面垂直⇒线线垂直;
(2)通过作出二面角的平面角,证明符合定义,再在三角形中求解.
解答:解析:(1)连接OC,由3AD=BD知,点D为AO的中点,
又∵AB为圆的直径,∴AC⊥BC,
∵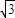 AC=BC,∴∠CAB=60°,
AC=BC,∴∠CAB=60°,
∴△ACO为等边三角形,∴CD⊥AO.
∵点P在圆O所在平面上的正投影为点D,
∴PD⊥平面ABC,又CD?平面ABC,
∴PD⊥CD,PD∩AO=D,
∴CD⊥平面PAB,PA?平面PAB,
∴PA⊥CD.
(2)过点D作DE⊥PB,垂足为E,连接CE,
由(1)知CD⊥平面PAB,又PB?平面PAB,
∴CD⊥PB,又DE∩CD=D,
∴PB⊥平面CDE,又CE?平面CDE,
∴CE⊥PB,
∴∠DEC为二面角C-PB-A的平面角.
由(1)可知CD=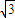 ,PD=BD=3,
,PD=BD=3,
∴PB=3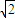 ,则DE=
,则DE=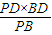 =
=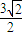 ,
,
∴在Rt△CDE中,tan∠DEC=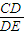 =
=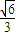 ,
,
∴cos∠DEC=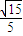 ,即二面角C-PB-A的余弦值为
,即二面角C-PB-A的余弦值为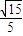 .
.
点评:本题考查线线垂直的判定、二面角的平面角及求法.二面角的求法:法1、作角(根据定义作二面角的平面角)--证角(符合定义)--求角(解三角形);
法2、空间向量法,求得两平面的法向量,再利用向量的数量积公式求夹角的余弦值.
(2)通过作出二面角的平面角,证明符合定义,再在三角形中求解.
解答:解析:(1)连接OC,由3AD=BD知,点D为AO的中点,
又∵AB为圆的直径,∴AC⊥BC,

∵
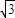 AC=BC,∴∠CAB=60°,
AC=BC,∴∠CAB=60°,∴△ACO为等边三角形,∴CD⊥AO.
∵点P在圆O所在平面上的正投影为点D,
∴PD⊥平面ABC,又CD?平面ABC,
∴PD⊥CD,PD∩AO=D,
∴CD⊥平面PAB,PA?平面PAB,
∴PA⊥CD.
(2)过点D作DE⊥PB,垂足为E,连接CE,
由(1)知CD⊥平面PAB,又PB?平面PAB,

∴CD⊥PB,又DE∩CD=D,
∴PB⊥平面CDE,又CE?平面CDE,
∴CE⊥PB,
∴∠DEC为二面角C-PB-A的平面角.
由(1)可知CD=
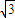 ,PD=BD=3,
,PD=BD=3,∴PB=3
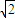 ,则DE=
,则DE=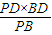 =
=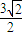 ,
,∴在Rt△CDE中,tan∠DEC=
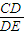 =
=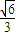 ,
,∴cos∠DEC=
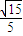 ,即二面角C-PB-A的余弦值为
,即二面角C-PB-A的余弦值为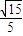 .
.点评:本题考查线线垂直的判定、二面角的平面角及求法.二面角的求法:法1、作角(根据定义作二面角的平面角)--证角(符合定义)--求角(解三角形);
法2、空间向量法,求得两平面的法向量,再利用向量的数量积公式求夹角的余弦值.

练习册系列答案
相关题目
 A:如图所示,已知AB为⊙O的直径,AC为弦,OD∥BC,交AC于点D,BC=4cm,
A:如图所示,已知AB为⊙O的直径,AC为弦,OD∥BC,交AC于点D,BC=4cm, (2013•潮州二模)如图所示,已知AB为圆O的直径,点D为线段AB上一点,且AD=
(2013•潮州二模)如图所示,已知AB为圆O的直径,点D为线段AB上一点,且AD=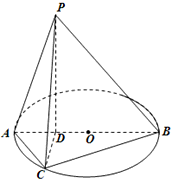 如图所示,已知AB为圆O的直径,点D为线段AB上一点,且AD=
如图所示,已知AB为圆O的直径,点D为线段AB上一点,且AD= DB,点C为圆O上一点,且BC=
DB,点C为圆O上一点,且BC= AC.点P在圆O所在平面上的正投影为点D,PD=DB.
AC.点P在圆O所在平面上的正投影为点D,PD=DB.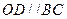 ,交AC于点D,BC=4cm,
,交AC于点D,BC=4cm,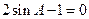 ,求⊙O的直径.
,求⊙O的直径.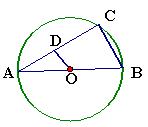
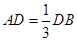 ,点C为圆O上一点,且
,点C为圆O上一点,且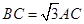 .点P在圆O所在平面上的正投影为点D,PD=DB.
.点P在圆O所在平面上的正投影为点D,PD=DB.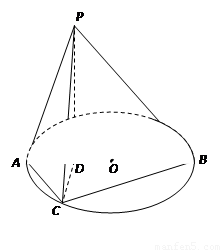
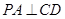 ;
;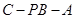 的余弦值.
的余弦值.