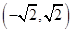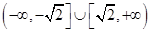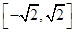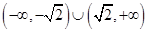题目内容
设函数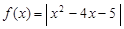 .
.
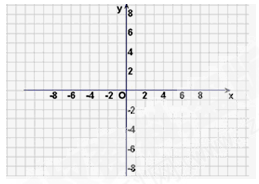
(1)在区间 上画出函数
上画出函数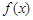 的图象 ;
的图象 ;
(2)设集合 . 试判断集合
. 试判断集合 和
和 之间的关系,并给出证明.
之间的关系,并给出证明.
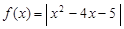 .
.
(1)在区间
 上画出函数
上画出函数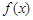 的图象 ;
的图象 ;(2)设集合
 . 试判断集合
. 试判断集合 和
和 之间的关系,并给出证明.
之间的关系,并给出证明.(1)详见解析; (2)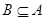 .
.
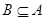 .
.试题分析:(1)根据函数的具体特点采用列表描点的基本方法,区间
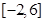 的端点
的端点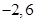 要单独考虑,另外还要考虑到函数
要单独考虑,另外还要考虑到函数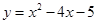 的零点,含有绝对值函数
的零点,含有绝对值函数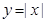 的图象的规律:
的图象的规律: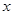 轴上方的不变,
轴上方的不变,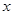 轴下方的翻到
轴下方的翻到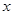 轴上方,这样就可画出函数在区间
轴上方,这样就可画出函数在区间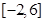 上的图象; (2)由不等式
上的图象; (2)由不等式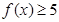 可转化为求出方程
可转化为求出方程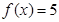 的根,再结合(1)中所作函数的图象,利用函数图象的单调性,即可确定出不等式
的根,再结合(1)中所作函数的图象,利用函数图象的单调性,即可确定出不等式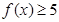 的解集
的解集 ,借助于数轴可分析
,借助于数轴可分析 出的关系.
出的关系.试题解析:(1)函数
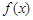 在区间
在区间 上画出的图象如下图所示:
上画出的图象如下图所示: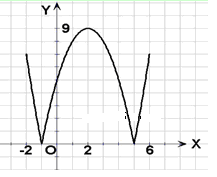 5分
5分(2)方程
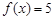 的解分别是
的解分别是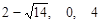 和
和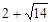 ,由于
,由于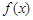 在
在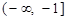 和
和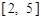 上单调递减,在
上单调递减,在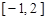 和
和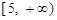 上单调递增,因此
上单调递增,因此 . 8分
. 8分由于
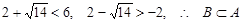 . 10分
. 10分
练习册系列答案
相关题目
 ,A
,A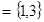 ,B
,B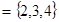 ,那么
,那么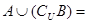 __.
__.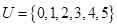 ,集合
,集合 ,
,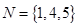 ,则集合
,则集合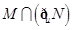 等于( )
等于( ) 的定义域为
的定义域为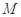 ,函数
,函数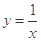 的定义域为
的定义域为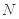 ,则
,则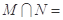 ( )
( )

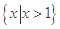
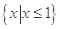
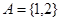 ,
,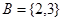 ,则
,则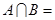 .
.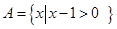 ,
,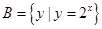 ,则
,则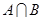 =
=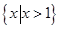
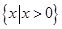
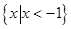
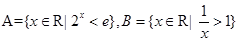 则
则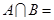 ( )
( )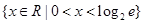
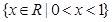
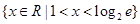
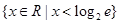
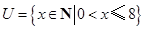 ,
,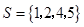 ,
,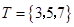 ,则
,则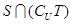 =( )
=( )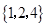
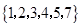
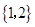
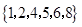
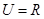 ,集合
,集合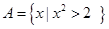 ,则
,则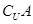 是( )
是( )