题目内容
设A=xn+x-n,B=xn-1+x1-n,当x∈R+,n∈N时,试比较A、B的大小.
A-B=(xn+x-n)-(xn-1+x1-n)
=x-n(x2n+1-x2n-1-x)=x-n[x(x2n-1-1)-(x2n-1-1)]
=x-n(x-1)(x2n-1-1).
由x∈R+,x-n>0,得当x≥1时,x-1≥0,x2n-1-1≥0;
当x<1时,x-1<0,x2n-1-1<0,即
x-1与x2n-1-1同号.∴A-B≥0,即A≥B.
=x-n(x2n+1-x2n-1-x)=x-n[x(x2n-1-1)-(x2n-1-1)]
=x-n(x-1)(x2n-1-1).
由x∈R+,x-n>0,得当x≥1时,x-1≥0,x2n-1-1≥0;
当x<1时,x-1<0,x2n-1-1<0,即
x-1与x2n-1-1同号.∴A-B≥0,即A≥B.
略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
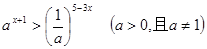 ,求
,求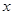 的取值范围.
的取值范围.  则关于
则关于 的不等式
的不等式 的解集是( )
的解集是( ) B
B
 D
D
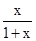
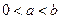 ,且
,且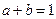 ,下列不等式中,一定成立的是
,下列不等式中,一定成立的是 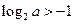 ;②
;②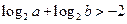 ;③
;③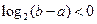 ;④
;④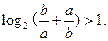
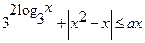 的解集为空集,则实数a的取值范围为__________
的解集为空集,则实数a的取值范围为__________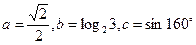 ,则
,则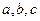 的大小关系为( )
的大小关系为( )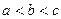
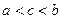
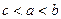
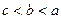
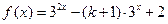 ,当
,当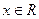 时,
时,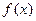 恒为正,则
恒为正,则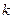 的取值范围是( ).
的取值范围是( ).


