题目内容
(08年长郡中学一模文)(13分)在平面直角坐标系中,已知定圆F:![]() (F为圆心),定直线
(F为圆心),定直线![]() ,作与圆F内切且和直线
,作与圆F内切且和直线![]() 相切的动圆P,
相切的动圆P,
(1)试求动圆圆心P的轨迹E的方程。
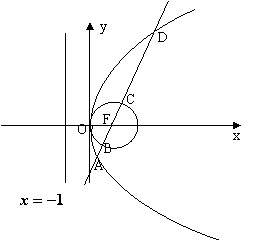
(2)设过定圆心F的直线![]() 自下而上依次交轨迹E及定园F于点A、B、C、D,
自下而上依次交轨迹E及定园F于点A、B、C、D,
①是否存在直线![]() ,使得
,使得![]() 成立?若存在,请求出这条直线的方程;若不存在,请说明理由。
成立?若存在,请求出这条直线的方程;若不存在,请说明理由。
②当直线![]() 绕点F转动时,
绕点F转动时,![]() 的值是否为定值?若是,请求出这个定值;若不是,请说明理由。
的值是否为定值?若是,请求出这个定值;若不是,请说明理由。

解析:(1)设动圆心P(x,y)
因为动圆P与定园F内切,则![]()
若![]() 则
则![]()
若![]() 则
则![]()
故动圆心P的轨迹是以F为焦点,![]() 为准线的抛物线,
为准线的抛物线,
其方程为:![]() ……4分
……4分
(2) ①当直线m的斜率存在, 由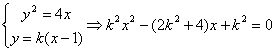
设![]() 则
则![]()
![]() 而
而![]()
若![]() 则
则![]() 无解,此时不存在。 ……8分
无解,此时不存在。 ……8分
当直线m的斜率不存在时,则![]() ,显然
,显然![]() 成立.
成立.
故存在直线m使![]() 成立.此时直线m:
成立.此时直线m:![]() ……9分
……9分
②当直线m的斜率存在时,由①![]()
当直线m的斜率不存在时,
![]()
故对于任意的直线m,![]() 为定值. ……13分
为定值. ……13分

练习册系列答案
相关题目