题目内容
6.设P,Q为一个正方体表面上的两点,已知此正方体绕着直线PQ旋转θ(0<θ<2π)角后能与自身重合,那么符合条件的直线PQ有13条.分析 由正方体自身的对称性可知,若正方体绕着直线PQ旋转θ(0<θ<2π)角后能与自身重合,则PQ比过正方体中心,由此分三种情况,即P,Q为正方体一体对角线两顶点时,P,Q为正方两相对棱中点时,P,Q为正方体对面中心时求得符合条件的直线PQ的条数.
解答 解:若正方体绕着直线PQ旋转θ(0<θ<2π)角后能与自身重合,则PQ比过正方体中心,否则,正方体绕着直线PQ旋转θ(0<θ<2π)角后,中心不能回到原来的位置.
共有三种情况:如图,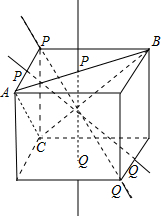
当P,Q为正方体一体对角线两顶点时,把正方体绕PQ旋转$\frac{2π}{3},\frac{4π}{3}$,正方体回到原来的位置,此时直线共有4条;
当P,Q为正方两相对棱中点时,把正方体绕PQ旋转π,正方体回到原来的位置,此时直线共有6条;
当P,Q为正方体对面中心时,把正方体绕PQ旋转$\frac{π}{2},π,\frac{3π}{2}$,正方体回到原来的位置,此时直线共有3条.
综上,符合条件的直线PQ有4+6+3=13条.
故答案为:13.
点评 本题考查了棱柱的结构特征,考查了学生的空间想象和思维能力,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$为单位向量,$\overrightarrow{a}$•$\overrightarrow{b}$=$\frac{1}{2}$,向量$\overrightarrow{c}$满足$\overrightarrow{a}$-$\overrightarrow{c}$与$\overrightarrow{b}$-$\overrightarrow{c}$的夹角为$\frac{π}{6}$,则|$\overrightarrow{a}$-$\overrightarrow{c}$|的最大值为( )
| A. | $\frac{3}{2}$ | B. | 4 | C. | $\frac{5}{2}$ | D. | 2 |
11.k棱柱有f(k)个对角面,则k+1棱柱的对角面个数f(k+1)为( )
| A. | f(k)+k-1 | B. | f(k)+k+1 | C. | f(k)+k | D. | f(k)+k-2 |
18.若方程2x3-6x2+6+m=0有三个不同的实数根,则m的取值范围( )
| A. | (-6,0) | B. | (-6,2) | C. | (-2,0) | D. | (0,6) |
16.已知a∈{1,2,3,4},b∈{1,2,3},则关于x的不等式x2-2(a-1)x+b2≥0的解集为R的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |




 如图,在三棱锥S-ABC中,底面ABC是正三角形,AB=4,SA=SC=2$\sqrt{3}$,侧面SAC⊥底面ABC,D,E分别为AB,SB的中点.
如图,在三棱锥S-ABC中,底面ABC是正三角形,AB=4,SA=SC=2$\sqrt{3}$,侧面SAC⊥底面ABC,D,E分别为AB,SB的中点.