题目内容
今年我国部分省市出现了人感染H7N9禽流感确诊病例,各地家禽市场受其影响生意冷清.A市虽未发现H7N9疑似病例,但经抽样有20%的市民表示还会购买本地家禽.现将频率视为概率,解决下列问题:
(Ⅰ)从该市市民中随机抽取3位,求至少有一位市民还会购买本地家禽的概率;
(Ⅱ)从该市市民中随机抽取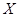 位,若连续抽取到两位愿意购买本地家禽的市民,或抽取的人数达到4位,则停止抽取,求
位,若连续抽取到两位愿意购买本地家禽的市民,或抽取的人数达到4位,则停止抽取,求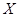 的分布列及数学期望.
的分布列及数学期望.
【答案】
(Ⅰ)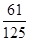 ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.
【解析】
试题分析:(Ⅰ)利用事件“该市市民中随机抽取3位,至少有一位市民还会购买本地家禽”的对立事件“该市市民中随机抽取3位,没有一位市民会购买本地家禽”,对立事件只有一种情况,而事件本身有3种基本情况,这样就方便了计算,算出对立事件的概率后,再根据对立事件与原事件的概率之和为1即可求出原事件的概率;(Ⅱ)先把随机变量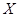 的可能值列出来,然后按照相应的
的可能值列出来,然后按照相应的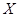 值利用排列组合的相关知识求对应的概率,列出相应的概率分布列进行计算即可.
值利用排列组合的相关知识求对应的概率,列出相应的概率分布列进行计算即可.
试题解析:(Ⅰ)依题意可得,任意抽取一位市民会购买本地家禽的概率为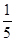 ,
,
从而任意抽取一位市民不会购买本地家禽的概率为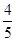 .
.
设“至少有一位市民会购买本地家禽”为事件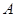 ,则
,则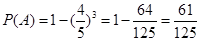 ,
,
故至少有一位市民会购买本地家禽的概率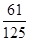 .
6分
.
6分
(Ⅱ)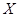 的所有可能取值为:2,3,4.
的所有可能取值为:2,3,4.
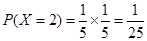 ,
,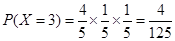 ,
,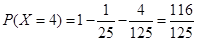 ,
,
所以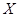 的分布列为:
的分布列为:
|
|
2 |
3 |
4 |
|
|
|
|
|
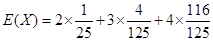
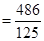 .
13分
.
13分
考点:二项分布、离散型随机变量的分布列与数学期望

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
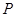
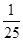
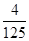
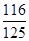
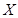 位,若连续抽取到两位愿意购买本地家禽的市民,或
位,若连续抽取到两位愿意购买本地家禽的市民,或