题目内容
已知f(x)=(x+1)(x+2)(x+3)…(x+n),(n≥2,n∈N),其导函数为f′(x),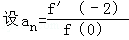 ,则a100= .
,则a100= .
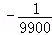
解析试题分析:由函数f(x)=(x+1)(x+2)(x+3)…(x+n),(n≥2,n∈N),求其导函数,得f′(x)=(x+2)(x+3)…(x+n)+(x+1)(x+3)…(x+n)+…+(x+1)(x+2)…(x+n﹣1),从而得f′(﹣2),f(0);由an= ,求得a100
,求得a100
∵函数f(x)=(x+1)(x+2)(x+3)…(x+n),(n≥2,n∈N),则
其导函数f′(x)=(x+2)(x+3)…(x+n)+(x+1)(x+3)…(x+n)+…+(x+1)(x+2)…(x+n﹣1),
∴f′(﹣2)=0+(﹣1)×1×…×(n﹣2)+0+…+0=﹣(n﹣2)!,f(0)=n!;
当an= 时,有a100=
时,有a100=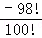 =﹣
=﹣
考点:数列与函数的综合
点评:本题考查了函数与数列的综合运用,并且重点考查了当函数解析式为多项式的积时的求导应用和阶乘的计算;是基础题

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 则
则 .
. 与
与 的图像关于直线
的图像关于直线 对称,则
对称,则 .
. 的图象与
的图象与 的图象关于直线
的图象关于直线 对称,则函数
对称,则函数 )处的切线方程为 .
)处的切线方程为 . 且
且 有两个零点,则实数
有两个零点,则实数 的取值范围是 .
的取值范围是 . 是奇函数,则a= 。
是奇函数,则a= 。 的所有零点之和为 .
的所有零点之和为 . 的定义域是__________。
的定义域是__________。 的单调减区间是 .
的单调减区间是 .