题目内容
设集合A={(x,y)|x2+y2≤9},B={(x, y)|
|
分析:根据题意可知,是与面积有关的几何概率,要求M落在区域Ω2内的概率,只要求A、B所表示区域的面积,然后代入概率公式 P=
,计算即可得答案.
| 区域Ω2的面积 |
| 区域Ω1的面积 |
解答: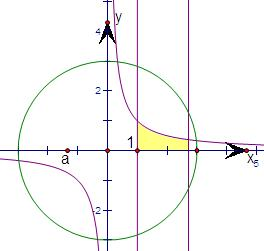 解:根据题意可得集合A={(x,y)|x2+y2≤9}所表示的区域即为如图所表示的圆及内部的平面区域,面积为9π,
解:根据题意可得集合A={(x,y)|x2+y2≤9}所表示的区域即为如图所表示的圆及内部的平面区域,面积为9π,
集合B={(x, y)|
表示的平面区域即为图中的阴影部分,其面积为:
∫1ex-1dx=lnx|1e=1,
根据几何概率的计算公式可得P=
,
故答案为:
.
 解:根据题意可得集合A={(x,y)|x2+y2≤9}所表示的区域即为如图所表示的圆及内部的平面区域,面积为9π,
解:根据题意可得集合A={(x,y)|x2+y2≤9}所表示的区域即为如图所表示的圆及内部的平面区域,面积为9π,集合B={(x, y)|
|
∫1ex-1dx=lnx|1e=1,
根据几何概率的计算公式可得P=
| 1 |
| 9π |
故答案为:
| 1 |
| 9π |
点评:本题主要考查了几何概率的计算公式P=
,而本题是与面积有关的几何概率模型.解决本题的关键是要准确求出两区域的面积.
| 基本事件所构成区域的长度、面积、体积 |
| 试验的全部结果所构成的区域的长度、面积、体积 |

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
设集合A=B={(x,y)|x∈R,y∈R},从A到B的映射f:(x,y)→(x+2y,2x-y),则在映射f下B中的元素(1,1)对应的A中元素为( )
| A、(1,3) | ||||
| B、(1,1) | ||||
C、(
| ||||
D、(
|



