题目内容
设f(x),g(x)分别是定义在R上的奇函数和偶函数.当x<0时,f′(x)g(x)+f(x)g′(x)> 0,且g(-3)=0,则不等式f(x)g(x)<0的解集是( )
| A.(-3,0)∪(3,+∞) | B.(-3,0)∪(0,3) |
| C.(-∞,-3)∪(3,+∞) | D.(-∞,-3)∪(0,3) |
D
试题分析:因为
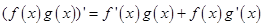 ,则由已知可得
,则由已知可得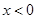 时,
时,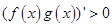 ,令
,令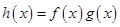 ,则函数
,则函数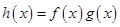 在
在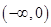 上单调递增。因为
上单调递增。因为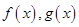 分别是在
分别是在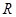 上的奇函数和偶函数,所以
上的奇函数和偶函数,所以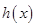 在
在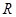 上是奇函数。则
上是奇函数。则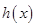 图像关于原点对称,且在
图像关于原点对称,且在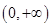 上也单调递增。因为
上也单调递增。因为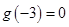 ,且
,且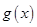 为偶函数则
为偶函数则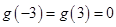 ,即
,即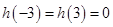 。综上可得
。综上可得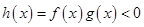 的解集为
的解集为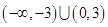 。故D正确。
。故D正确。
练习册系列答案
相关题目
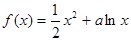 ,
,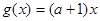 .
.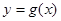 恰好为曲线
恰好为曲线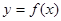 的切线时,求实数
的切线时,求实数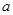 的值;
的值;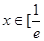 ,
,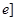 时(其中无理数
时(其中无理数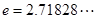 ),
),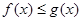 恒成立,试确定实数
恒成立,试确定实数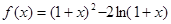
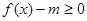 在
在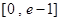 有实数解,求实数m的取值范围;
有实数解,求实数m的取值范围;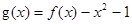 ,若关于x的方程
,若关于x的方程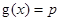 至少有一个解,求p的最小值.
至少有一个解,求p的最小值.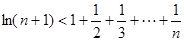
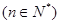
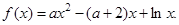
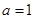 时,求曲线
时,求曲线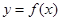 在点
在点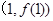 处的切线方程;
处的切线方程;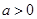 时,若
时,若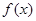 在区间
在区间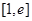 上的最小值为-2,求
上的最小值为-2,求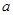 的取值范围;
的取值范围; 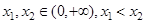 ,且
,且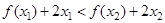 恒成立,求
恒成立,求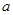 为实数,函数
为实数,函数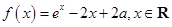 .
.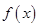 的单调区间与极值;
的单调区间与极值; 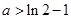 且
且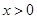 时,
时,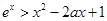 .
.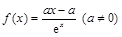
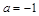 时,求函数
时,求函数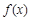 的极值;
的极值;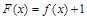 没有零点,求实数a取值范围.
没有零点,求实数a取值范围.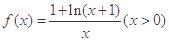
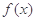 在区间
在区间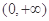 上是增函数还是减函数?证明你的结论;
上是增函数还是减函数?证明你的结论;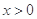 时,
时,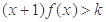 恒成立,求整数
恒成立,求整数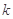 的最大值;
的最大值;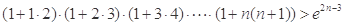 (
(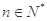 )
) 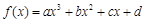 的图象如图所示,则
的图象如图所示,则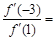 ( )
( )
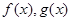 都是定义在R上的函数,
都是定义在R上的函数,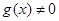 ,
,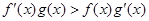 ,且
,且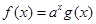
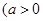 ,且
,且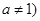 ,
,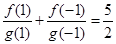 .若数列
.若数列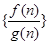 的前n项和大于62,则n的最小值为( )
的前n项和大于62,则n的最小值为( )