题目内容
已知函数y=x2-4|x|+5在（-∞，a）内单调递减，则实数a的取值范围是（ ）A．a≥-2
B．a≤-2
C．a≥0
D．a≤2
【答案】分析：先对函数y=x2-4|x|+5取绝对值，画出其对应的图象，利用图象来找实数a的取值范围即可．
解答：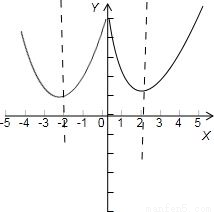
解：因为y=x2-4|x|+5=
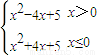其图象如图．
由图得，函数y=x2-4|x|+5在（-∞，a）内单调递减区间为（-∞，-2]，
故实数a的取值范围是a≤-2．
故选B．
点评：本题考查了二次函数的图象，通过图象来找函数的单调区间，数形结合有助于我们的解题，形象直观．
解答：
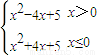解：因为y=x2-4|x|+5=其图象如图．由图得，函数y=x2-4|x|+5在（-∞，a）内单调递减区间为（-∞，-2]，
故实数a的取值范围是a≤-2．
故选B．
点评：本题考查了二次函数的图象，通过图象来找函数的单调区间，数形结合有助于我们的解题，形象直观．
练习册系列答案
相关题目
已知函数y=x2-4|x|+5在（-∞，a）内单调递减，则实数a的取值范围是（ ）
| A、a≥-2 | B、a≤-2 | C、a≥0 | D、a≤2 |