题目内容
在研究色盲与性别的关系调查中,调查了男性480人,其中有38人患色盲,调查的520名女性中有6人患色盲.
(1)根据以上数据建立一个2×2列联表;
(2)若认为“性别与患色盲有关系”,则出错的概率会是多少?
随机变量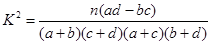
附临界值参考表:
(1)根据以上数据建立一个2×2列联表;
| | 患色盲 | 不患色盲 | 总计 |
| 男 | | 442 | |
| 女 | 6 | | |
| 总计 | 44 | 956 | 1000 |
随机变量
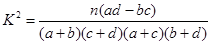
附临界值参考表:
| P(K2≥x0) | 0.10 | 0.05 | 0.025 | 0.10 | 0.005 | 0.001 |
| x0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(1)
(2)“性别与患色盲有关系”,则出错的概率为0.1%
| | 患色盲 | 不患色盲 | 总计 |
| 男 | 38 | 442 | 480 |
| 女 | 6 | 514 | 520 |
| 总计 | 44 | 956 | 1 000 |
试题分析:(1)
| | 患色盲 | 不患色盲 | 总计 |
| 男 | 38 | 442 | 480 |
| 女 | 6 | 514 | 520 |
| 总计 | 44 | 956 | 1 000 |
K2=
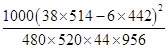 ≈27.14, 8分
≈27.14, 8分又P(K2≥10.828)=0.001,即H0成立的概率不超过0.001, 11分
故若认为“性别与患色盲有关系”,则出错的概率为0.1%. 12分
点评:解决的关键是利用反证法思想来得到判错率,属于基础题。

练习册系列答案
相关题目
 为学校因为该学员而奖励教官的金额数,求
为学校因为该学员而奖励教官的金额数,求
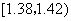
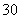
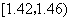
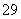
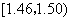
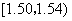
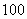
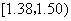 中的概率及纤度小于
中的概率及纤度小于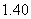 的概率是多少?
的概率是多少?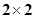 的列联表;(2)能否在犯错误的概率不超过0.05的前提下认为晕机与性别有关?
的列联表;(2)能否在犯错误的概率不超过0.05的前提下认为晕机与性别有关? 的列联表;
的列联表;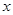 (单位:万元)与销售额
(单位:万元)与销售额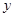 (单位:万元)之间有如下对应数据:
(单位:万元)之间有如下对应数据: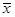 ,
,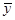 的值并求点
的值并求点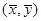 对应的复数
对应的复数 ;
; 。
。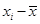
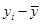
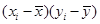
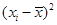
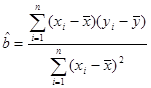 )
)
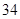
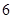
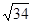
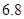
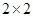 列联表进行独立性检验,经计算
列联表进行独立性检验,经计算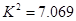 ,则所得到的统计学结论是:有( )的把握认为“学生性别与支持该活动有关系”。
,则所得到的统计学结论是:有( )的把握认为“学生性别与支持该活动有关系”。
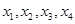 的方差为
的方差为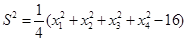 ,则数据
,则数据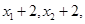
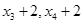 的平均数为( )
的平均数为( )