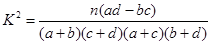题目内容
在生产过程中,测得纤维产品的纤度(表示纤维粗细的一种量)共有100个数据,将数据分组如表:
(1)列出频率分布表,并画出频率分布直方图;
(2)估计纤度落在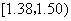 中的概率及纤度小于
中的概率及纤度小于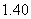 的概率是多少?
的概率是多少?
(3)从频率分布直方图估计出纤度的众数、中位数和平均数.
| 分组 | 频数 |
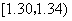 | 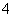 |
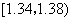 | 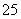 |
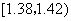 | 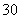 |
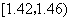 | 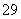 |
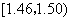 | 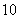 |
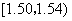 | 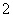 |
| 合计 | 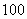 |
(2)估计纤度落在
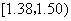 中的概率及纤度小于
中的概率及纤度小于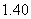 的概率是多少?
的概率是多少?(3)从频率分布直方图估计出纤度的众数、中位数和平均数.
(1)
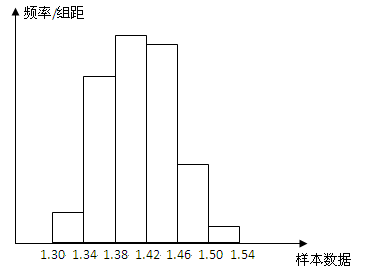
(2)0.44
(3)总体数据的众数:1.40, 中位数:1.408,平均数1.4088
| 分组 | 频数 | 频率 |
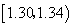 | 4 | 0.04 |
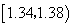 | 25 | 0.25 |
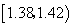 | 30 | 0.30 |
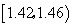 | 29 | 0.29 |
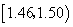 | 10 | 0.10 |
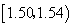 | 2 | 0.02 |
| 合计 | 100 | 1.00 |

(2)0.44
(3)总体数据的众数:1.40, 中位数:1.408,平均数1.4088
试题分析:(Ⅰ)根据题意,由于纤维产品的纤度(表示纤维粗细的一种量)共有100个数据,那么结合频率等于频数与样本容量的比值来得到,那么可知
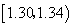 的频率为
的频率为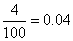 ,在区间
,在区间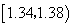 的频率为
的频率为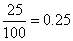 ,依次可知为
,依次可知为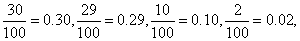 ,那么可知表格为:
,那么可知表格为:| 分组 | 频数 | 频率 |
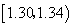 | 4 | 0.04 |
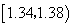 | 25 | 0.25 |
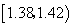 | 30 | 0.30 |
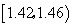 | 29 | 0.29 |
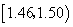 | 10 | 0.10 |
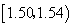 | 2 | 0.02 |
| 合计 | 100 | 1.00 |

(2)纤度落在
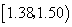 中的概率约为
中的概率约为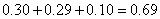 ,
,纤度小于1.40的概率约为
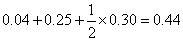 .
.(Ⅲ)总体数据的众数:1.40 中位数:1.408
平均数:
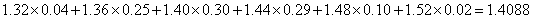 .
.点评:主要是考查了统计中直方图的应用,以及数据来估计总体的应用,属于基础题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
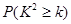
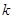
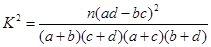 ,其中
,其中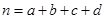 )
)