题目内容
已知集合M＝{-1，1，0}，N＝{2，3，4，5}，映射f：M→N，当x∈M时，x+f(x)+xf(x)为奇数，则这样的映射f的个数是
- A.20
- B.18
- C.32
- D.24
C
当x＝0时，f(x)必须为奇数，则有f(x)＝3或5，故有两种映射方式：
当x＝-1时，x+f(x)+xf(x)＝-1+f(-1)-f(-1)＝-1为奇数，
故有4种映射方式：
当x＝1时，x+f(x)+xf(x)＝1+2f(1)为奇数，故有4种映射方式．
故映射个数为2×4×4＝32(个)，选C．
当x＝0时，f(x)必须为奇数，则有f(x)＝3或5，故有两种映射方式：
当x＝-1时，x+f(x)+xf(x)＝-1+f(-1)-f(-1)＝-1为奇数，
故有4种映射方式：
当x＝1时，x+f(x)+xf(x)＝1+2f(1)为奇数，故有4种映射方式．
故映射个数为2×4×4＝32(个)，选C．
练习册系列答案
相关题目
，集合A中所有元素的乘积称为集合A的“累积值”，且规定：当集合A只有一个元素时，其累积值即为该元素的数值，空集的累积值为0. 设集合A的累积值为n.
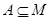，集合A中所有元素的乘积称为集合A