题目内容
已知函数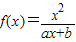 (a,b为常数)且方程f(x)-x+12=0有两个实根为x1=3,x2=4.
(a,b为常数)且方程f(x)-x+12=0有两个实根为x1=3,x2=4.(1)求函数f(x)的解析式;
(2)设k>1,解关于x的不等式;
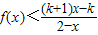 .
.
【答案】分析:(1)将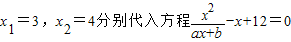 得出关于a,b的方程组,解之即得a,b,从而得出函数f(x)的解析式.
得出关于a,b的方程组,解之即得a,b,从而得出函数f(x)的解析式.
(2)不等式即为:即(x-2)(x-1)(x-k)>0.下面对k进行分类讨论:①当1<k<2,②当k=2时,③当k>2时,分别求出此不等式的解集即可.
解答:解:(1)将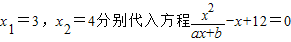 得
得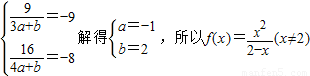 .
.
(2)不等式即为
即(x-2)(x-1)(x-k)>0.
①当1<k<2,解集为x∈(1,k)∪(2,+∞).
②当k=2时,不等式为(x-2)2(x-1)>0解集为x∈(1,2)∪(2,+∞);
③当k>2时,解集为x∈(1,2)∪(k,+∞).
点评:本题主要是应用分类讨论思想解决不等式问题,关键是正确地进行分类,而分类一般有以下几个原则:
1.要有明确的分类标准;
2.对讨论对象分类时要不重复、不遗漏,即分成若干类,其并集为全集,两两的交集为空集;
3.当讨论的对象不止一种时,应分层次进行,以避免混乱.根据绝对值的意义判断出f(x)的奇偶性,再利用偶函数的图象关于y轴对称,求出函数在(0,+∞)上的单调区间,并且只要求出当x>0时,函数f(x)=x2-2ax(a>0)最小值进而利用f(x)min≤-1解答此题.
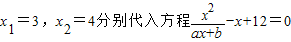 得出关于a,b的方程组,解之即得a,b,从而得出函数f(x)的解析式.
得出关于a,b的方程组,解之即得a,b,从而得出函数f(x)的解析式.(2)不等式即为:即(x-2)(x-1)(x-k)>0.下面对k进行分类讨论:①当1<k<2,②当k=2时,③当k>2时,分别求出此不等式的解集即可.
解答:解:(1)将
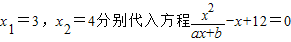 得
得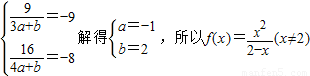 .
.(2)不等式即为

即(x-2)(x-1)(x-k)>0.
①当1<k<2,解集为x∈(1,k)∪(2,+∞).
②当k=2时,不等式为(x-2)2(x-1)>0解集为x∈(1,2)∪(2,+∞);
③当k>2时,解集为x∈(1,2)∪(k,+∞).
点评:本题主要是应用分类讨论思想解决不等式问题,关键是正确地进行分类,而分类一般有以下几个原则:
1.要有明确的分类标准;
2.对讨论对象分类时要不重复、不遗漏,即分成若干类,其并集为全集,两两的交集为空集;
3.当讨论的对象不止一种时,应分层次进行,以避免混乱.根据绝对值的意义判断出f(x)的奇偶性,再利用偶函数的图象关于y轴对称,求出函数在(0,+∞)上的单调区间,并且只要求出当x>0时,函数f(x)=x2-2ax(a>0)最小值进而利用f(x)min≤-1解答此题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
 ,则
,则