题目内容
(本题满分12)
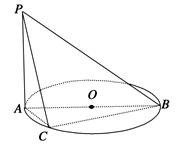
如图,在三棱锥S-ABC中,ΔABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=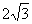 ,M,N分别为AB,SB的中点。
,M,N分别为AB,SB的中点。
(Ⅰ)求异面直线AC与SB所成角; (Ⅱ)求二面角 N-CM-B的大小;
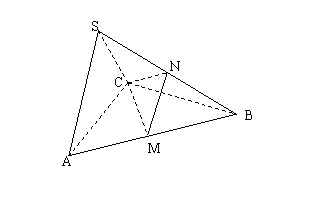 (Ⅲ)求点B到平面CMN的距离。
(Ⅲ)求点B到平面CMN的距离。
【答案】
解:
(I)取AC 中点D,连结SD,DB。
因为SA=SC,AB=BC,所以AC⊥SD且AC⊥BD,所以AC⊥平面SDB.
又SB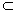 平面SDB,所以AC⊥SB.所以异面直线AC与SB所成角为90
平面SDB,所以AC⊥SB.所以异面直线AC与SB所成角为90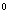 。…………4分
。…………4分
(II)因为AC⊥平面SDB,AC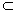 平面ABC, 所以平面SDC⊥平面ABC.
平面ABC, 所以平面SDC⊥平面ABC.
过N作NE⊥BD于E,则NE⊥平面ABC,
过E作EF⊥CM于F,连结NF,则NF⊥CM,
所以∠NFE为二面角N-CM-B的平面角。
因为平面SAC⊥平面ABC, SD⊥AC,所以SD⊥平面ABC.
又因为NE⊥平面ABC,所以NE∥SD。
由于SN=NB,所以NE=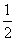 SD=
SD=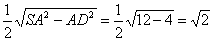 ,且ED=EB.
,且ED=EB.
在正△ABC中,由平面几何知识可求得EF=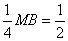 .
.
在Rt△NEF中,tan∠NFE=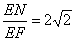
所以二面角N-CM-B的大小是arctan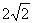 .
………………………………8分
.
………………………………8分
(III)在Rt△NEF中,NF=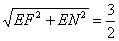 ,所以
,所以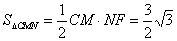 ,
,
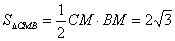 .
.
设点B到平面CMN的距离为h,
因为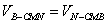 ,NE⊥平面CMB,
,NE⊥平面CMB,
所以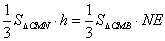 则h=
则h=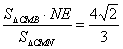
即点B到平面CMN的距离为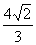 。
………………………………12分
。
………………………………12分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A2处时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距10
海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A2处时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距10
 ⊥矩形
⊥矩形 所在的平面,
所在的平面, 分别是
分别是 、
、 的中点,
的中点,
 ∥平面
∥平面 ;
; ;
; ,求证:平面
,求证:平面 ⊥平面
⊥平面 .
. M、N分别是
M、N分别是 CD.
CD. ,求直线AC与平面BCD所成的角.
,求直线AC与平面BCD所成的角.
 的底面
的底面 是正方形,侧面
是正方形,侧面 是等腰三角形且垂直于底面,
是等腰三角形且垂直于底面, ,
, ,
, 、
、 分别是
分别是 、
、 的中点。
的中点。 ;
; 的大小。
的大小。