题目内容
如图,已知棱长为1的正方体ABCD-A1B1C1D1.(1)线段A1B上是否存在一点P,使得A1B⊥平面PAC?若存在,确定P点的位置,若不存在,说明理由;
(2)点P在A1B上,若二面角C-AP-B的大小是arctan2,求BP的长;
(3)Q点在对角线B1D,使得A1B∥平面QAC,求
 .
.
【答案】分析:(1)线段A1B上不存在一点P,使得A1B⊥平面PAC.用反证明法进行证明.
(2)作出平面角∠BHC,由 ,知∠HAB=30°,在△ABP中用正弦定理可得BP=
,知∠HAB=30°,在△ABP中用正弦定理可得BP= .
.
(3)A1B∥平面D1AC,Q是B1D与平面ACD1的交点,△B1D1Q∽△DOQ,由此能求出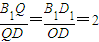 .
.
解答:解: (1)线段A1B上不存在一点P,使得A1B⊥平面PAC.
(1)线段A1B上不存在一点P,使得A1B⊥平面PAC.
理由如下:
假设线段A1B上是否存在一点P,使得A1B⊥平面PAC.
结AC,则AC⊥A1B.
∵AA1⊥AC,
∴AC⊥面AA1B1B,
∴AC⊥AB,与∠BAC=45°矛盾.
∴线段A1B上不存在一点P,使得A1B⊥平面PAC.
(2)∵CB⊥平面ABP,作BN⊥AP,交AH延长线与H,连接CH,
则∠BHC是二面角二面角C-AP-B平面角…(6分)
∵二面角C-AP-B的大小是arctan2,
∴tan∠BHC= ,即
,即 ,
,
∴∠HAB=30°…(8分)
在△ABP中,
∠PAB=30°,AB=1,∠PBA=45°,
∴∠APB=180°-30°-45°=105°,
由正弦定理,得 ,
,
∴
= =
= .
.
∴BP= …(10分)
…(10分)
(3)∵A1B∥平面D1AC,
Q是B1D与平面ACD1的交点,…(12分)
△B1D1Q∽△DOQ,
∴ …(14分).
…(14分).
点评:本题考查立体几何的综合运用,考查考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,易出错.
(2)作出平面角∠BHC,由
 ,知∠HAB=30°,在△ABP中用正弦定理可得BP=
,知∠HAB=30°,在△ABP中用正弦定理可得BP= .
.(3)A1B∥平面D1AC,Q是B1D与平面ACD1的交点,△B1D1Q∽△DOQ,由此能求出
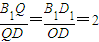 .
.解答:解:
 (1)线段A1B上不存在一点P,使得A1B⊥平面PAC.
(1)线段A1B上不存在一点P,使得A1B⊥平面PAC.理由如下:
假设线段A1B上是否存在一点P,使得A1B⊥平面PAC.
结AC,则AC⊥A1B.
∵AA1⊥AC,
∴AC⊥面AA1B1B,
∴AC⊥AB,与∠BAC=45°矛盾.
∴线段A1B上不存在一点P,使得A1B⊥平面PAC.
(2)∵CB⊥平面ABP,作BN⊥AP,交AH延长线与H,连接CH,
则∠BHC是二面角二面角C-AP-B平面角…(6分)
∵二面角C-AP-B的大小是arctan2,
∴tan∠BHC=
 ,即
,即 ,
,∴∠HAB=30°…(8分)
在△ABP中,
∠PAB=30°,AB=1,∠PBA=45°,
∴∠APB=180°-30°-45°=105°,
由正弦定理,得
 ,
,∴

=
 =
= .
.∴BP=
 …(10分)
…(10分)(3)∵A1B∥平面D1AC,
Q是B1D与平面ACD1的交点,…(12分)
△B1D1Q∽△DOQ,
∴
 …(14分).
…(14分).点评:本题考查立体几何的综合运用,考查考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,易出错.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 如图,已知棱长为1的正方体ABCD-A1B1C1D1中,E是A1B1的中点,则直线AE与平面ABC1D1所成的角的正弦值是( )
如图,已知棱长为1的正方体ABCD-A1B1C1D1中,E是A1B1的中点,则直线AE与平面ABC1D1所成的角的正弦值是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,已知棱长为1的正方体容器ABCD-A1B1C1D1,在棱AB以及B1C的中点处各有一个小孔E、G,在B1处有一个小孔,若此容器可以任意放置,则该容器可装水的最大容积为
如图,已知棱长为1的正方体容器ABCD-A1B1C1D1,在棱AB以及B1C的中点处各有一个小孔E、G,在B1处有一个小孔,若此容器可以任意放置,则该容器可装水的最大容积为 如图,已知棱长为1的正方体ABCD-A1B1C1D1.
如图,已知棱长为1的正方体ABCD-A1B1C1D1.