题目内容
在一次抗洪抢险中,准备用射击的方法引爆从桥上游漂流而下的一巨大汽油罐.已知只有5发子弹备用,且首次命中只能使汽油流出,再次命中才能引爆成功,每次射击命中率都是(1)求油罐被引爆的概率.
(2)如果引爆或子弹打光则停止射击,设射击次数为ξ,求ξ的分布列及ξ的数学期望;
解:(1)记“油罐被引爆”的事件为事件A,其对立事件为![]() ,?
,?
则P(A)=C15·(![]() )(
)(![]() )4+(
)4+(![]() )5. ?
)5. ?
∴P(A)=1-[C15·(![]() )·(
)·(![]() )4+(
)4+(![]() )5]=
)5]=![]() . ?
. ?
(2)射击次数ξ的可能取值为2,3,4,5.?
P(ξ=2)=(![]() )2=
)2=![]() , ?
, ?
P(ξ=3)=C12·![]() ·
·![]() ·
·![]() =
=![]() , ?
, ?
P(ξ=4)=C13·![]() (
(![]() )2·
)2·![]() =
=![]() , ?
, ?
P(ξ=5)=C14·(![]() )(
)(![]() )3+(
)3+(![]() )4=
)4=![]() . ?
. ?
故ξ的分布列为
ξ | 2 | 3 | 4 | 5 |
P |
|
|
|
|
?
Eξ=2×![]() +3×
+3×![]() +4×
+4×![]() +5×
+5×![]() =
=![]() .
.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
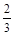 .,每次命中与否互相独立.
.,每次命中与否互相独立.