题目内容
若函数y=ax+2的图象与函数y=
x-
的图象关于直线y=x对称,则logab的值是( )
| 1 |
| 2 |
| b |
| 4 |
A.-
| B.
| C.1 | D.2 |
∵y=ax+2的图象与y=
x-
的图象关于直线y=x对称,
∴y=ax+2图象上任一点P(x,ax+2)关于y=x对称点Q(ax+2,x)必在y=
x-
的图象上.
故对一切实数x总有x=
(ax+2)-
,
∴
?
.
则logab=则log24=2.
故选D.
| 1 |
| 2 |
| b |
| 4 |
∴y=ax+2图象上任一点P(x,ax+2)关于y=x对称点Q(ax+2,x)必在y=
| 1 |
| 2 |
| b |
| 4 |
故对一切实数x总有x=
| 1 |
| 2 |
| b |
| 4 |
∴
|
|
则logab=则log24=2.
故选D.

练习册系列答案
相关题目
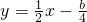 的图象关于直线y=x对称,则logab的值是
的图象关于直线y=x对称,则logab的值是
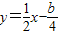 的图象关于直线y=x对称,则logab的值是( )
的图象关于直线y=x对称,则logab的值是( )

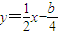 的图象关于直线y=x对称,则logab的值是( )
的图象关于直线y=x对称,则logab的值是( )
