题目内容
【题目】己知无穷数列![]() 的前
的前![]() 项和为
项和为![]() ,若对于任意的正整数
,若对于任意的正整数![]() ,均有
,均有![]() ,则称数列
,则称数列![]() 具有性质
具有性质![]() .
.
(1)判断首项为![]() ,公比为
,公比为![]() 的无穷等比数列
的无穷等比数列![]() 是否具有性质
是否具有性质![]() ,并说明理由;
,并说明理由;
(2)己知无穷数列![]() 具有性质
具有性质![]() ,且任意相邻四项之和都相等,求证:
,且任意相邻四项之和都相等,求证:![]() ;
;
(3)己知![]() ,数列
,数列![]() 是等差数列,
是等差数列,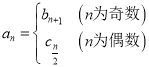 ,若无穷数列
,若无穷数列![]() 具有性质
具有性质![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)答案见解析(2)证明见解析(3)![]()
【解析】
(1)因为首项为![]() ,公比为
,公比为![]() 的无穷等比数列
的无穷等比数列![]() ,即可
,即可![]() ,求
,求![]() 和
和![]() ,即可求得答案;
,即可求得答案;
(2)因为无穷数列![]() 具有性质
具有性质![]() ,且任意相邻四项之和都相等,
,且任意相邻四项之和都相等,![]() 满足周期性,且
满足周期性,且![]() ,可得
,可得![]() ,因为
,因为![]() 具备性质
具备性质![]() ,故满足:
,故满足:![]() ,
,![]() ,采用反证法证明,即可求得答案;
,采用反证法证明,即可求得答案;
(3)数列![]() 是等差数列,可得
是等差数列,可得![]() 的前
的前![]() 项和为:
项和为:![]() ,因为
,因为![]() 前
前![]() 项和为:
项和为:![]() ,由
,由![]() 具备性质
具备性质![]() ,则
,则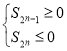 其中
其中![]() 中包含
中包含![]() 项奇数项,
项奇数项,![]() 项偶数项,结合已知,即可求得答案.
项偶数项,结合已知,即可求得答案.
(1)![]() 首项为
首项为![]() ,公比为
,公比为![]() 的无穷等比数列
的无穷等比数列![]()
![]()
![]()
根据等比数列前![]() 项和公式可得:
项和公式可得:
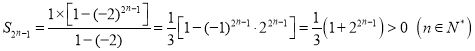 ,
,

![]() 数列
数列![]() 满足具有性质
满足具有性质![]() .
.
(2)![]() 无穷数列
无穷数列![]() 具有性质
具有性质![]() ,且任意相邻四项之和都相等
,且任意相邻四项之和都相等
![]()
![]() 满足周期性,且
满足周期性,且![]()
可得![]()
![]()
![]() 具备性质
具备性质![]()
![]() 满足:
满足:![]() ,
,![]()
利用反正法证明:
若![]() ,则
,则![]() ,
,
令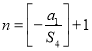
![]() 得:
得:![]() (注:当
(注:当![]() 时,
时,![]() ,则当
,则当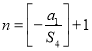 时,
时,![]() )
)
与![]() 矛盾.
矛盾.
![]()
![]() ,
,
又![]()
![]() ,
,
![]()
![]() .证明完毕.
.证明完毕.
(3)![]() 数列
数列![]() 是等差数列
是等差数列
![]()
![]() 的前
的前![]() 项和为:
项和为:![]() ,
,
![]()
![]() 前
前![]() 项和为:
项和为:![]()
由![]() 具备性质
具备性质![]() ,
,
则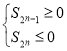
其中![]() 中包含
中包含![]() 项奇数项,
项奇数项,![]() 项偶数项,
项偶数项,
有:![]()
![]()
![]()
其中![]() 中包含
中包含![]() 项奇数项,
项奇数项,![]() 项偶数项,
项偶数项,
故:![]()
![]()
![]()
由性质![]()
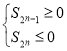
可得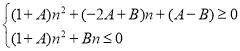 ,对任意
,对任意![]() 成立
成立
![]()
![]() 、
、![]() 满足:
满足: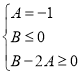 ,解得:
,解得:![]()
![]()
![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某学校有30位高级教师,其中60%人爱好体育锻炼,经体检调查,得到如下列联表.
身体好 | 身体一般 | 总计 | |
爱好体育锻炼 | 2 | ||
不爱好体育锻炼 | 4 | ||
总计 | 20 |
(1)根据以上信息完成![]() 列联表,并判断有多大把握认为“身体好与爱好体育锻炼有关系”?
列联表,并判断有多大把握认为“身体好与爱好体育锻炼有关系”?
(2)现从身体一般的教师中抽取3人,记3人中爱好体育锻炼的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
参考公式: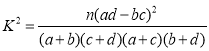 ,其中
,其中![]() .
.
临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |