题目内容
定义两种运算:,a⊕b=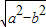 ,a?b=
,a?b=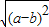 ,则函数f(x)=
,则函数f(x)= 的解析式为( )
的解析式为( )A.f(x)=-
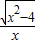 ,x∈(-∞,-2]∪[2,+∞)
,x∈(-∞,-2]∪[2,+∞)B.f(x)=
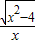 ,x∈(-∞,-2]∪[2,+∞)
,x∈(-∞,-2]∪[2,+∞)C.f(x)=-
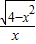 ,x∈[-2,0)∪(0,2]
,x∈[-2,0)∪(0,2]D.f(x)=
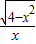 ,x∈[-2,0)∪(0,2]
,x∈[-2,0)∪(0,2]
【答案】分析:由已知中a⊕b= ,a?b=
,a?b= ,我们可以得到
,我们可以得到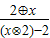 的表达式,进而根据函数定义域的确定原则,可以求出函数的定义域,结合函数的定义域,化简函数的解析式后,即可得到答案.
的表达式,进而根据函数定义域的确定原则,可以求出函数的定义域,结合函数的定义域,化简函数的解析式后,即可得到答案.
解答:解:∵a⊕b=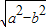 ,a?b=
,a?b=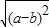
∴函数f(x)=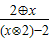 =
=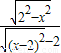 ,(x∈[-2,0)∪(0,2])
,(x∈[-2,0)∪(0,2])
又∵当x∈[-2,0)∪(0,2]时,
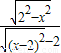 =
=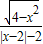 =
=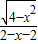 =
=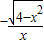
故函数f(x)=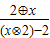 的解析式为f(x)=-
的解析式为f(x)=-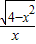 ,x∈[-2,0)∪(0,2]
,x∈[-2,0)∪(0,2]
故选C
点评:本题以函数解析式的求法为载体考查了函数的定义域及根式与分式的化简,其中根据新定义确定函数的解析式,并根据解析式分析函数的定义域是解答的关键.
 ,a?b=
,a?b= ,我们可以得到
,我们可以得到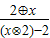 的表达式,进而根据函数定义域的确定原则,可以求出函数的定义域,结合函数的定义域,化简函数的解析式后,即可得到答案.
的表达式,进而根据函数定义域的确定原则,可以求出函数的定义域,结合函数的定义域,化简函数的解析式后,即可得到答案.解答:解:∵a⊕b=
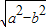 ,a?b=
,a?b=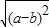
∴函数f(x)=
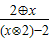 =
=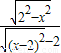 ,(x∈[-2,0)∪(0,2])
,(x∈[-2,0)∪(0,2])又∵当x∈[-2,0)∪(0,2]时,
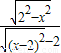 =
=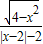 =
=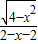 =
=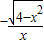
故函数f(x)=
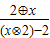 的解析式为f(x)=-
的解析式为f(x)=-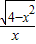 ,x∈[-2,0)∪(0,2]
,x∈[-2,0)∪(0,2]故选C
点评:本题以函数解析式的求法为载体考查了函数的定义域及根式与分式的化简,其中根据新定义确定函数的解析式,并根据解析式分析函数的定义域是解答的关键.

练习册系列答案
相关题目
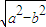 ,a?b=
,a?b=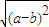 ,则函数f(x)=
,则函数f(x)=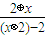 的解析式为( )
的解析式为( )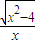 ,x∈(-∞,-2]∪[2,+∞)
,x∈(-∞,-2]∪[2,+∞)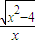 ,x∈(-∞,-2]∪[2,+∞)
,x∈(-∞,-2]∪[2,+∞)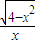 ,x∈[-2,0)∪(0,2]
,x∈[-2,0)∪(0,2]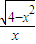 ,x∈[-2,0)∪(0,2]
,x∈[-2,0)∪(0,2]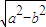 ,a?b=
,a?b=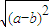 ,则函数f(x)=
,则函数f(x)=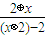 的解析式为( )
的解析式为( )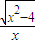 ,x∈(-∞,-2]∪[2,+∞)
,x∈(-∞,-2]∪[2,+∞)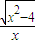 ,x∈(-∞,-2]∪[2,+∞)
,x∈(-∞,-2]∪[2,+∞)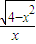 ,x∈[-2,0)∪(0,2]
,x∈[-2,0)∪(0,2]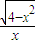 ,x∈[-2,0)∪(0,2]
,x∈[-2,0)∪(0,2]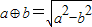 ,a*b=|a-b|,则函数
,a*b=|a-b|,则函数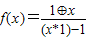 的奇偶性为( )
的奇偶性为( )