题目内容
定义两种运算: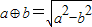 ,a*b=|a-b|,则函数
,a*b=|a-b|,则函数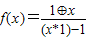 的奇偶性为( )
的奇偶性为( )A.奇函数
B.偶函数
C.既是奇函数又是偶函数
D.既非奇函数又非偶函数
【答案】分析:由题意可得f(x)=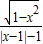 =-
=-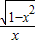 ,利用奇偶函数的定义判断即可.
,利用奇偶函数的定义判断即可.
解答:解:∵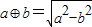 ,a*b=|a-b|,
,a*b=|a-b|,
∴f(x)=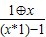 =
=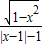 ,
,
∵1-x2≥0,|x-1|-1≠0,
∴-1≤x<0或0<x≤1,
∴f(x)=-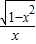 ,
,
∴f(-x)=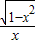 =-f(x),
=-f(x),
∴f(x)为奇函数.
故选A.
点评:本题考查函数函数奇偶性的判断,将f(x)化为f(x)=-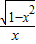 是关键,
是关键,
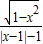 =-
=-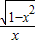 ,利用奇偶函数的定义判断即可.
,利用奇偶函数的定义判断即可.解答:解:∵
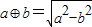 ,a*b=|a-b|,
,a*b=|a-b|,∴f(x)=
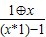 =
=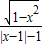 ,
,∵1-x2≥0,|x-1|-1≠0,
∴-1≤x<0或0<x≤1,
∴f(x)=-
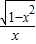 ,
,∴f(-x)=
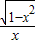 =-f(x),
=-f(x),∴f(x)为奇函数.
故选A.
点评:本题考查函数函数奇偶性的判断,将f(x)化为f(x)=-
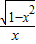 是关键,
是关键, 
练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
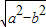 ,a?b=
,a?b=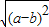 ,则函数f(x)=
,则函数f(x)= 的解析式为( )
的解析式为( )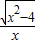 ,x∈(-∞,-2]∪[2,+∞)
,x∈(-∞,-2]∪[2,+∞)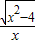 ,x∈(-∞,-2]∪[2,+∞)
,x∈(-∞,-2]∪[2,+∞)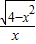 ,x∈[-2,0)∪(0,2]
,x∈[-2,0)∪(0,2]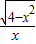 ,x∈[-2,0)∪(0,2]
,x∈[-2,0)∪(0,2]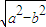 ,a?b=
,a?b=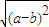 ,则函数f(x)=
,则函数f(x)=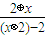 的解析式为( )
的解析式为( )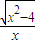 ,x∈(-∞,-2]∪[2,+∞)
,x∈(-∞,-2]∪[2,+∞)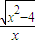 ,x∈(-∞,-2]∪[2,+∞)
,x∈(-∞,-2]∪[2,+∞)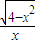 ,x∈[-2,0)∪(0,2]
,x∈[-2,0)∪(0,2]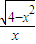 ,x∈[-2,0)∪(0,2]
,x∈[-2,0)∪(0,2]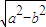 ,a?b=
,a?b=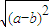 ,则函数f(x)=
,则函数f(x)=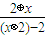 的解析式为( )
的解析式为( )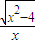 ,x∈(-∞,-2]∪[2,+∞)
,x∈(-∞,-2]∪[2,+∞)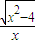 ,x∈(-∞,-2]∪[2,+∞)
,x∈(-∞,-2]∪[2,+∞)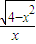 ,x∈[-2,0)∪(0,2]
,x∈[-2,0)∪(0,2]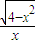 ,x∈[-2,0)∪(0,2]
,x∈[-2,0)∪(0,2]